
【題目】現代足球運動是世上開展得最廣泛、影響最大的運動項目,有人稱它為“世界第一運動”.早在2000多年前的春秋戰國時代,就有了一種球類游戲“蹴鞠”,后來經過阿拉伯人傳到歐洲,發展成現代足球.1863年10月26日,英國人在倫敦成立了世界上第一個足球運動組織——英國足球協會,并統一了足球規則.人們稱這一天是現代足球的誕生日.如圖所示,足球表面是由若干黑色正五邊形和白色正六邊形皮圍成的,我們把這些正五邊形和正六邊形都稱為足球的面,任何相鄰兩個面的公共邊叫做足球的棱.已知足球表面中的正六邊形的面為20個,則該足球表面中的正五邊形的面為______個,該足球表面的棱為______條.

【答案】12 90
【解析】
由題目分析,可設這個足球有正五邊形皮子x塊,則根據題意可得等量關系式:正六邊形的塊數×3=正五邊形的塊數×5,由此可以解出正五邊形個數,根據兩條邊組成一條棱,因此可求棱的條數.
足球每塊黑色皮子的5條邊分別與5塊白色皮子的邊縫在一起;
每塊白色皮子的6條邊中,有3條邊與黑色皮子的邊縫在一起,
另3條邊則與其他白色皮子的邊縫在一起.
所以設這個足球有x塊正五邊形,一共有5x條邊,其中白皮三條邊和黑皮相連,
又足球表面中的正六邊形的面為20個,
根據題意可得方程:![]() ,
,
解得![]() ,
,
該足球表面中的正五邊形的面為12個;
因為任何相鄰兩個面的公共邊叫做足球的棱,
所以每條棱由兩條邊組成,
該足球表面的棱為:![]() 條.
條.
故答案為:12;90.


 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:
【題目】已知非常數列![]() 滿足
滿足![]() ,若
,若![]() ,則( )
,則( )
A.存在![]() ,
,![]() ,對任意
,對任意![]() ,
,![]() ,都有
,都有![]() 為等比數列
為等比數列
B.存在![]() ,
,![]() ,對任意
,對任意![]() ,
,![]() ,都有
,都有![]() 為等差數列
為等差數列
C.存在![]() ,
,![]() ,對任意
,對任意![]() ,
,![]() ,都有
,都有![]() 為等差數列
為等差數列
D.存在![]() ,
,![]() ,對任意
,對任意![]() ,
,![]() ,都有
,都有![]() 為等比數列
為等比數列
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,是由矩形![]() ,
,![]() 和
和![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() ,
,![]() ,將其沿
,將其沿![]() 折起使得
折起使得![]() 重合,連接
重合,連接![]() 如圖②.
如圖②.
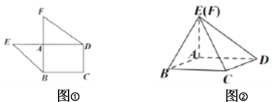
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() 中點,求直線
中點,求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,在
,在![]() 軸上,是否存在點
軸上,是否存在點![]() ,使得無論非零實數
,使得無論非零實數![]() 怎樣變化,總有
怎樣變化,總有![]() 為直角?若存在,求出點
為直角?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫務人員說:“包括我在內,我們社區診所醫生和護士共有16名.無論是否把我算在內,下面說法都是對的.在這些醫務人員中:護士多于醫生;女醫生多于女護士;女護士多于男護士;至少有一名男醫生.”請你推斷說話的人的性別與職業是( )
A.男醫生B.女醫生C.男護士D.女護士
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com