
已知數列{an}滿足a1>0,an+1=2-|an|,n∈N*.
(1)若a1,a2,a3成等比數列,求a1的值;
(2)是否存在a1,使數列{an}為等差數列?若存在,求出所有這樣的a1;若不存在,說明理由.
(1)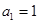 或
或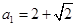 (2)
(2)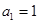
解析試題分析:(1)首先利用遞推公式把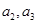 都用
都用 表示,再根據
表示,再根據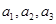 成等比數列,列方程解出
成等比數列,列方程解出 的值,注意根據絕對值的定義要對
的值,注意根據絕對值的定義要對 的取值范圍分類計論.
的取值范圍分類計論.
(2)對于這類開放性問題,處理的策略就是先假設存在a1,使數列{an}為等差數列,與(1)類似,根據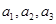 成等差數列,有
成等差數列,有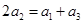 ,從面得到關于
,從面得到關于 的方程,方程若有解則存在,否則可認為不存在a1,使數列{an}為等差數列.
的方程,方程若有解則存在,否則可認為不存在a1,使數列{an}為等差數列.
試題解析:(1)∵a1>0,∴a2=2-|a1|=2-a1,a3=2-|a2|=2-|2-a1|.
當0<a1≤2時,a3=2-(2-a1)=a1,∴a12=(2-a1)2,解得a1=1.
當a1>2時,a3=2-(a1-2)=4-a1,∴a1(4-a1)=(2-a1)2,解得a1=2- (舍去)或a1=2+
(舍去)或a1=2+ .
.
綜上可得a1=1或a1=2+ . 6分
. 6分
(2)假設這樣的等差數列存在,則
由2a2=a1+a3,得2(2-a1)=a1+(2-|2-a1|),即|2-a1|=3a1-2.
當a1>2時,a1-2=3a1-2,解得a1=0,與a1>2矛盾;
當0<a1≤2時,2-a1=3a1-2,解得a1=1,從而an=1(n∈N*),此時{an}是一個等差數列;
綜上可知,當且僅當a1=1時,數列{an}為等差數列. 12分
考點:1、等差數列、等比數列的定義;2、分類討論的思想.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:解答題
已知數列{an}的首項為a1=1,其前n項和為Sn,且對任意正整數n有n,an,Sn成等差數列.
(1)求證:數列{Sn+n+2}成等比數列.
(2)求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知首項為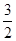 的等比數列{an}不是遞減數列,其前n項和為Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差數列.
的等比數列{an}不是遞減數列,其前n項和為Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差數列.
(1)求數列{an}的通項公式;
(2)設Tn=Sn- (n∈N*),求數列{Tn}的最大項的值與最小項的值.
(n∈N*),求數列{Tn}的最大項的值與最小項的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知n∈N*,數列{dn}滿足dn=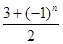 ,數列{an}滿足an=d1+d2+d3+…+d2n,又知在數列{bn}中,b1=2,且對任意正整數m,n,
,數列{an}滿足an=d1+d2+d3+…+d2n,又知在數列{bn}中,b1=2,且對任意正整數m,n, .
.
(1)求數列{an}和數列{bn}的通項公式;
(2)將數列{bn}中的第a1項,第a2項,第a3項,…,第an項,…刪去后,剩余的項按從小到大的順序排成新數列{cn},求數列{cn}的前2 013項和.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在等差數列{an}中,a16+a17+a18=a9=-36,其前n項和為Sn.
(1)求Sn的最小值,并求出Sn取最小值時n的值;
(2)求Tn=|a1|+|a2|+…+|an|.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列 中,
中, ,
, ,
, .
.
(1)證明:數列 是等比數列,并求數列
是等比數列,并求數列 的通項公式;
的通項公式;
(2)在數列 中,是否存在連續三項成等差數列?若存在,求出所有符合條件的項;若不存在,請說明理由;
中,是否存在連續三項成等差數列?若存在,求出所有符合條件的項;若不存在,請說明理由;
(3)若 且
且 ,
, ,求證:使得
,求證:使得 ,
, ,
, 成等差數列的點列
成等差數列的點列 在某一直線上.
在某一直線上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com