
【題目】已知橢圓C:![]() (a>b>0)的左右焦點分別為F1,F2點.M為橢圓上的一動點,△MF1F2面積的最大值為4.過點F2的直線l被橢圓截得的線段為PQ,當l⊥x軸時,
(a>b>0)的左右焦點分別為F1,F2點.M為橢圓上的一動點,△MF1F2面積的最大值為4.過點F2的直線l被橢圓截得的線段為PQ,當l⊥x軸時,![]() .
.
(1)求橢圓C的方程;
(2)過點F1作與x軸不重合的直線l,l與橢圓交于A,B兩點,點A在直線![]() 上的投影N與點B的連線交x軸于D點,D點的橫坐標x0是否為定值?若是,求出定值;若不是,請說明理由.
上的投影N與點B的連線交x軸于D點,D點的橫坐標x0是否為定值?若是,求出定值;若不是,請說明理由.
科目:高中數學 來源: 題型:
【題目】波羅尼斯(古希臘數學家,約公元前262-190年)的著作《圓錐曲線論》是古代世界光輝的科學成果,它將圓錐曲線的性質網羅殆盡幾乎使后人沒有插足的余地.他證明過這樣一個命題:平面內與兩定點距離的比為常數k(![]() 且
且![]() )的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.現有
)的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.現有![]() ,
,![]() ,則當
,則當![]() 的面積最大時,AC邊上的高為_______________.
的面積最大時,AC邊上的高為_______________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以原點為極點,x軸的正半軸為極軸,建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為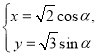 (α為參數).設曲線
(α為參數).設曲線![]() 與x軸、y軸的交點分別為A,B,線段
與x軸、y軸的交點分別為A,B,線段![]() 的中點為M,射線
的中點為M,射線![]() 與曲線
與曲線![]() 交于點N.
交于點N.
(1)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的極坐標方程;
的極坐標方程;
(2)求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中將底面為直角三角形且側棱垂直于底面的三棱柱稱為“塹堵”;底面為矩形,一條側棱垂直于底面的四棱錐稱之為“陽馬”;四個面均為直角三角形的四面體稱為“鱉膈”.如圖在塹堵ABC-A1B1C1中,AC⊥BC,且AA1=AB=2.下列說法正確的是( )
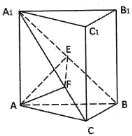
A.四棱錐B-A1ACC1為“陽馬”
B.四面體A1C1CB為“鱉膈”
C.四棱錐B-A1ACC1體積最大為![]()
D.過A點分別作AE⊥A1B于點E,AF⊥A1C于點F,則EF⊥A1B
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“海水稻”就是耐鹽堿水稻,是一種介于野生稻和栽培稻之間的普遍生長在海邊灘涂地區,具有耐鹽堿的水稻,它比其它普通的水稻均有更強的生存競爭能力,具有抗澇,抗病蟲害,抗倒伏等特點,還具有預防和治療多種疾病的功效,防癌效果尤為顯著.海水稻的灌溉是將海水稀釋后進行灌溉.某試驗基地為了研究海水濃度![]() (‰)對畝產量
(‰)對畝產量![]() (噸)的影響,通過在試驗田的種植實驗,測得了某種海水稻的畝產量與海水濃度的數據如表.繪制散點圖發現,可用線性回歸模型擬合畝產量
(噸)的影響,通過在試驗田的種植實驗,測得了某種海水稻的畝產量與海水濃度的數據如表.繪制散點圖發現,可用線性回歸模型擬合畝產量![]() 與海水濃度
與海水濃度![]() 之間的相關關系,用最小二乘法計算得
之間的相關關系,用最小二乘法計算得![]() 與
與![]() 之間的線性回歸方程為
之間的線性回歸方程為![]() .
.
海水濃度 | 3 | 4 | 5 | 6 | 7 |
畝產量 | 0.62 | 0.58 | 0.49 | 0.4 | 0.31 |
殘差 |
(1)請你估計:當澆灌海水濃度為8‰時,該品種的畝產量.
(2)①完成上述殘差表:
②統計學中,常用相關指數![]() 來刻畫回歸效果,
來刻畫回歸效果,![]() 越大,模型擬合效果越好,并用它來說明預報變量與解釋變量的相關性.你能否利用以上表格中的數據,利用統計學的相關知識,說明澆灌海水濃度對畝產量的貢獻率?(計算中數據精確到
越大,模型擬合效果越好,并用它來說明預報變量與解釋變量的相關性.你能否利用以上表格中的數據,利用統計學的相關知識,說明澆灌海水濃度對畝產量的貢獻率?(計算中數據精確到![]() )
)
(附:殘差公式![]() ,相關指數
,相關指數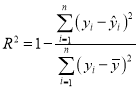 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張師傅欲將一球形的石材工件削砍加工成一圓柱形的新工件,已知原球形工件的半徑為![]() ,則張師傅的材料利用率的最大值等于(注:材料利用率=
,則張師傅的材料利用率的最大值等于(注:材料利用率=![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】設球半徑為R,圓柱的體積為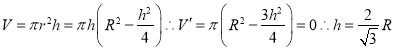 時圓柱的體積最大為
時圓柱的體積最大為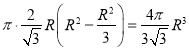 ,因此材料利用率=
,因此材料利用率=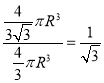 ,選C.
,選C.
點睛:空間幾何體與球接、切問題的求解方法
求解球與棱柱、棱錐的接、切問題時,一般過球心及接、切點作截面,把空間問題轉化為平面圖形與圓的接、切問題,再利用平面幾何知識尋找幾何中元素間的關系求解.
【題型】單選題
【結束】
12
【題目】已知拋物線![]() :
: ![]()
![]() 在點
在點![]() 處的切線與曲線
處的切線與曲線![]() :
: ![]() 相切,若動直線
相切,若動直線![]() 分別與曲線
分別與曲線![]() 、
、![]() 相交于
相交于![]() 、
、![]() 兩點,則
兩點,則![]() 的最小值為( )
的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨的十九大明確把精準脫貧作為決勝全面建成小康社會必須打好的三大攻堅戰之一,為堅決打贏脫貧攻堅戰,某幫扶單位考察了甲乙兩種不同的農產品加工生產方式,現對兩種生產方式加工的產品質量進行測試并打分對比,得到如下數據:
生產方式甲 | 分值區間 |
|
|
|
|
|
頻數 | 20 | 30 | 100 | 40 | 10 | |
生產方式乙 | 分值區間 |
|
|
|
|
|
頻數 | 25 | 35 | 50 | 30 |
其中產品質量按測試指標可劃分為:指標在區間![]() 上的為特優品,指標在區間
上的為特優品,指標在區間![]() 上的為一等品,指標在區間
上的為一等品,指標在區間![]() 上的為二等品.
上的為二等品.
(1)用事件![]() 表示“按照生產方式甲生產的產品為特優品”,估計
表示“按照生產方式甲生產的產品為特優品”,估計![]() 的概率;
的概率;
(2)填寫下面列聯表,并根據列聯表判斷能否有![]() 的把握認為“特優品”與生產方式有關?
的把握認為“特優品”與生產方式有關?
特優品 | 非特優品 | |
生產方式甲 | ||
生產方式乙 |
(3)根據打分結果對甲乙兩種生產方式進行優劣比較.
附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
參考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】健身館某項目收費標準為每次60元,現推出會員優惠活動:具體收費標準如下:
消費次數 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收費比例 | 0.95 | 0.90 | 0.85 | 0.80 |
現隨機抽取了100位會員統計它們的消費次數,得到數據如下:
消費次數 | 1次 | 2次 | 3次 | 不少于4次 |
頻數 | 60 | 25 | 10 | 5 |
假設該項目的成本為每次30元,根據給出的數據回答下列問題:
(1)估計1位會員至少消費兩次的概率
(2)某會員消費4次,求這4次消費獲得的平均利潤;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com