
【題目】在平面直角坐標(biāo)系![]() 中,拋物線
中,拋物線![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 的直線
的直線![]() 交
交![]() 于
于![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() 到
到![]() 軸的距離比
軸的距離比![]() 小
小![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若![]() ,求
,求![]() 的方程.
的方程.
【答案】:(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】試題分析:(Ⅰ)由拋物線的定義,可知![]() 等于點
等于點![]() 到
到![]() 的準(zhǔn)線的距離,即
的準(zhǔn)線的距離,即![]() ,又因為點
,又因為點![]() 到
到![]() 軸的距離比
軸的距離比![]() 小
小![]() ,所以
,所以![]() ,解出
,解出![]() 的方程為
的方程為![]()
(Ⅱ)由題意可設(shè)![]() 的方程為
的方程為![]() ),聯(lián)立方程組由韋達定理,得
),聯(lián)立方程組由韋達定理,得![]() 又
又![]() ,所以
,所以![]() ,所以
,所以![]() ,從而
,從而![]() ,即
,即![]() ,即可解出
,即可解出![]() ,寫出直線方程.
,寫出直線方程.
試題解析:(Ⅰ) ![]() 的準(zhǔn)線方程為
的準(zhǔn)線方程為![]() ,
,
由拋物線的定義,可知![]() 等于點
等于點![]() 到
到![]() 的準(zhǔn)線的距離,即
的準(zhǔn)線的距離,即![]() ,
,
又因為點![]() 到
到![]() 軸的距離比
軸的距離比![]() 小
小![]() ,
,
所以![]() ,
,
故![]() ,解得
,解得![]() ,
,
所以![]() 的方程為
的方程為![]()
(Ⅱ)由(Ⅰ)得![]() 的焦點
的焦點![]() ,因為直線
,因為直線![]() 交
交![]() 于
于![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,所以
,所以![]() 的斜率存在且不為
的斜率存在且不為![]() ,故可設(shè)
,故可設(shè)![]() 的方程為
的方程為![]() ,
,
則![]() .
.
聯(lián)立方程組![]() ,消去
,消去![]() ,得
,得![]()
![]() ,
,
由韋達定理,得![]()
設(shè)點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則
,則![]()
又![]() ,所以
,所以![]() .
.
又![]() 在同一直線上,所以
在同一直線上,所以![]() ,從而
,從而![]() ,即
,即![]() ,
,
因為![]() ,
,
所以![]() ,整理,得
,整理,得![]() ,
,
故![]() ,解得
,解得![]() ,
,
所以![]() 的方程為
的方程為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù) ![]() 是定義在(﹣1,1)上的奇函數(shù),且
是定義在(﹣1,1)上的奇函數(shù),且 ![]() .
.
(1)確定函數(shù)的解析式;
(2)證明函數(shù)f(x)在(﹣1,1)上是增函數(shù);
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=﹣x3+ax2+1,(a∈R).
(1)若f(x)圖象上橫坐標(biāo)為1的點處存在垂直于y軸的切線,求a的值;
(2)若f(x)在區(qū)間(﹣1,2)內(nèi)有兩個不同的極值點,求a取值范圍;
(3)當(dāng)a=1時,是否存在實數(shù)m,使得函數(shù)g(x)=x4﹣5x3+(2﹣m)x2+1的圖象于函數(shù)f(x)的圖象恰有三個不同的交點,若存在,試求出實數(shù)m的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點F(0,1),直線l:y=﹣1,P為平面上的動點,過點P作直線l的垂線,垂足為Q,且 ![]() .
.
(1)求動點P的軌跡C的方程;
(2)已知圓M過定點D(0,2),圓心M在軌跡C上運動,且圓M與x軸交于A、B兩點,設(shè)|DA|=l1 , |DB|=l2 , 求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】五一節(jié)期間,某商場為吸引顧客消費推出一項優(yōu)惠活動,活動規(guī)則如下:消費額每滿100元可轉(zhuǎn)動如圖所示的轉(zhuǎn)盤一次,并獲得相應(yīng)金額的返券.(假定指針等可能地停在任一位置,指針落在區(qū)域的邊界時,重新轉(zhuǎn)一次)指針?biāo)诘膮^(qū)域及對應(yīng)的返劵金額見表.
例如:消費218元,可轉(zhuǎn)動轉(zhuǎn)盤2次,所獲得的返券金額是兩次金額之和.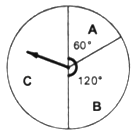
(1)已知顧客甲消費后獲得n次轉(zhuǎn)動轉(zhuǎn)盤的機會,已知他每轉(zhuǎn)一次轉(zhuǎn)盤指針落在區(qū)域邊界的概率為p,每次轉(zhuǎn)動轉(zhuǎn)盤的結(jié)果相互獨立,設(shè)ξ為顧客甲轉(zhuǎn)動轉(zhuǎn)盤指針落在區(qū)域邊界的次數(shù),ξ的數(shù)學(xué)期望Eξ= ![]() ,方差Dξ=
,方差Dξ= ![]() ,求n、p的值;
,求n、p的值;
(2)顧客乙消費280元,并按規(guī)則參與了活動,他獲得返券的金額記為η(元).求隨機變量η的分布列和數(shù)學(xué)期望.
指針位置 | A區(qū)域 | B區(qū)域 | C區(qū)域 |
返券金額(單位:元) | 60 | 30 | 0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
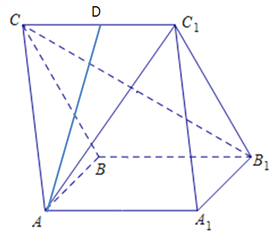
【題目】如圖所示,在三棱柱![]() 中,
中,![]() 為正方形,
為正方形,![]() 為菱形,
為菱形,![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 中點,
中點,![]() 是二面角
是二面角![]() 的平面角,求直線
的平面角,求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com