
分析 (1)根據方程x2+y2+Dx+Ey+F=0表示圓的條件,結合題意求出F的取值范圍;
(2)根據題意求出r和d,計算d2-r2的值即可;
(3)存在定圓M:x2+y2=1滿足題意,證明圓M與直線l相切,并且圓M與圓C相離即可.
解答 解:(1)方程x2+y2+Dx+Ey+F=0表示圓,
則D2+E2>4F,
又D2+E2=F2,且F>0,
所以中F2>4F,且F>0,
解得F>4; …(3分)
(2)圓C:x2+y2+Dx+Ey+F=0的圓心為C(-$\frac{D}{2}$,-$\frac{E}{2}$),
半徑r=$\frac{\sqrt{{D}^{2}{+E}^{2}-4F}}{2}$=$\frac{\sqrt{{F}^{2}-4F}}{2}$,
圓心C到直線l的距離為
d=$\frac{|D×(-\frac{D}{2})+E×(-\frac{E}{2})+F|}{\sqrt{{D}^{2}{+E}^{2}}}$=|$\frac{F-2}{2}$|,
所以d2-r2=${|\frac{F-2}{2}|}^{2}$-${(\frac{\sqrt{{F}^{2}-4F}}{2})}^{2}$=1; …(8分)
(3)存在定圓M:x2+y2=1滿足題意,下證之:…(10分)
1°因為M(0,0)到直線l的距離為$\frac{|F|}{\sqrt{{D}^{2}{+E}^{2}}}$=1=R,
所以圓M與直線l相切;
2°因為CM=$\sqrt{{(0+\frac{D}{2})}^{2}{+(0+\frac{E}{2})}^{2}}$=$\frac{F}{2}$,且R+1=$\frac{\sqrt{{F}^{2}-4F}}{2}$+1,
而$\frac{F}{2}$>$\frac{\sqrt{{F}^{2}-4F}}{2}$+1,
即${(\frac{F}{2}-1)}^{2}$>$\frac{{F}^{2}-4F}{4}$,
即4>0,
故CM>R+1,
所以圓M與圓C相離;
由1°、2°得,存在定圓M:x2+y2=1滿足題意. …(16分)
點評 本題考查了直線與圓的方程與應用問題,也考查了點到直線的距離問題的應用,是綜合性問題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
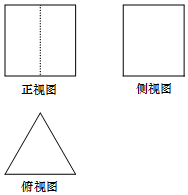 某幾何體的三視圖如圖所示,其中正視圖是邊長為2的正方形,俯視圖是正三角形,則這個幾何體的體積是( )
某幾何體的三視圖如圖所示,其中正視圖是邊長為2的正方形,俯視圖是正三角形,則這個幾何體的體積是( )| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
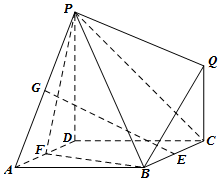 如圖所示的多面體中,面ABCD是邊長為2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分別為棱BC,AD,PA的中點.
如圖所示的多面體中,面ABCD是邊長為2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分別為棱BC,AD,PA的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
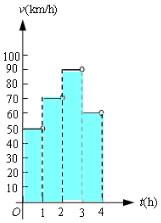 一輛汽車在某段路程中的行駛速率與時間的關系如圖所示.
一輛汽車在某段路程中的行駛速率與時間的關系如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖,直線l是曲線y=f(x)在x=3處的切線,f'(x)表示函數f(x)的導函數,則f(3)+f'(3)的值為$\frac{7}{3}$.
如圖,直線l是曲線y=f(x)在x=3處的切線,f'(x)表示函數f(x)的導函數,則f(3)+f'(3)的值為$\frac{7}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com