
【題目】對于定義域為D的函數![]() ,若存在區間
,若存在區間![]() ,使得
,使得![]() 同時滿足,①
同時滿足,①![]() 在
在![]() 上是單調函數,②當
上是單調函數,②當![]() 的定義域為
的定義域為![]() 時,
時,![]() 的值域也為
的值域也為![]() ,則稱區間
,則稱區間![]() 為該函數的一個“和諧區間”
為該函數的一個“和諧區間”
(1)求出函數![]() 的所有“和諧區間”
的所有“和諧區間”![]() ;
;
(2)函數![]() 是否存在“和諧區間”
是否存在“和諧區間”![]() ?若存在,求出實數a,b的值;若不存在,請說明理由
?若存在,求出實數a,b的值;若不存在,請說明理由
(3)已知定義在![]() 上的函數
上的函數![]() 有“和諧區間”,求正整數k取最小值時實數m的取值范圍.
有“和諧區間”,求正整數k取最小值時實數m的取值范圍.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)不存在;理由見解析;(3)
;(2)不存在;理由見解析;(3)![]()
【解析】
(1)根據“和諧”函數的定義,建立條件關系,即可求![]() 符合條件的“和諧”區間;
符合條件的“和諧”區間;
(2)判斷函數![]() 是否滿足“和諧”函數的條件即可;
是否滿足“和諧”函數的條件即可;
(3)根據函數![]() 是“和諧”函數,建立條件關系,即可求實數
是“和諧”函數,建立條件關系,即可求實數![]() 的取值范圍.
的取值范圍.
(1)因為函數![]() 在
在![]() 上單調遞增,
上單調遞增,
所以有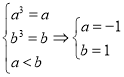 或
或![]() 或
或![]() ;
;
即![]() 或
或![]() 或
或![]() .
.
(2)畫出函數![]() 的圖象
的圖象
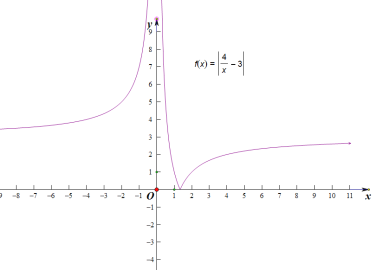
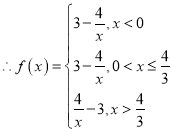
由圖可知函數在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
且函數值域為![]() ,故在
,故在![]() 上不存在 “和諧區間”;
上不存在 “和諧區間”;
假設函數在區間![]() 存在 “和諧區間”
存在 “和諧區間”![]() ,則
,則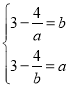 方程組無解,假設不成立;同理可得函數在區間
方程組無解,假設不成立;同理可得函數在區間![]() 也不存在 “和諧區間”。
也不存在 “和諧區間”。
故函數![]() 不存在 “和諧區間”。
不存在 “和諧區間”。
(3)![]() 在
在![]() 上有“和諧區間”,
上有“和諧區間”,
所以存在區間![]() ,使函數
,使函數![]() 的值域為
的值域為![]() ,
,
![]() 函數在
函數在![]() 上單調遞增
上單調遞增
![]() 在
在![]() 單調遞增,即
單調遞增,即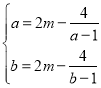 ,
,
![]() 為關于
為關于![]() 的方程
的方程![]() 的兩個實根,即方程
的兩個實根,即方程![]() 在
在![]() 上有兩個不等的實根,即
上有兩個不等的實根,即![]() 在
在![]() 上有兩個不等的實根,令
上有兩個不等的實根,令![]()
與![]() ,問題轉化為函數
,問題轉化為函數![]() 與
與![]() ,在
,在![]() 上存在兩個不同的交點.
上存在兩個不同的交點.
考察函數![]() 如圖
如圖
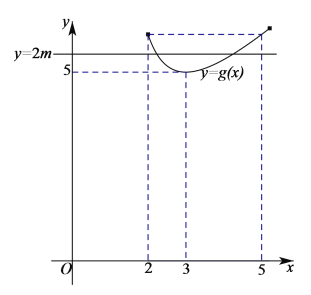
函數![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 上單調遞增.
上單調遞增.
![]() ,且
,且![]() ,
,
∵函數![]() 在
在![]() 上遞減,當
上遞減,當![]() 時,直線
時,直線![]() 與函數
與函數![]() 不可能有兩個交點,∴
不可能有兩個交點,∴![]()
∵![]() 在
在![]() 遞增,由圖象可知,當
遞增,由圖象可知,當![]() 時,函數
時,函數![]() 與
與![]() 在
在![]() 存在兩個交點,
存在兩個交點,
所以正整數![]() 的最小值為
的最小值為![]() ,
,![]() ,此時,
,此時,![]() ,解得
,解得![]() .
.
故![]() .
.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】【2018山西晉城市高三上學期一模】環境問題是當今世界共同關注的問題,我國環保總局根據空氣污染指數![]() 濃度,制定了空氣質量標準:
濃度,制定了空氣質量標準:
空氣污染指數 |
|
|
|
|
|
|
空氣質量等級 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
某市政府為了打造美麗城市,節能減排,從2010年開始考察了連續六年11月份的空氣污染指數,繪制了頻率分布直方圖,經過分析研究,決定從2016年11月1日起在空氣質量重度污染和嚴重污染的日子對機動車輛限號出行,即車牌尾號為單號的車輛單號出行,車牌尾號為雙號的車輛雙號出行(尾號是字母的,前13個視為單號,后13個視為雙號),王先生有一輛車,若11月份被限行的概率為0.05.
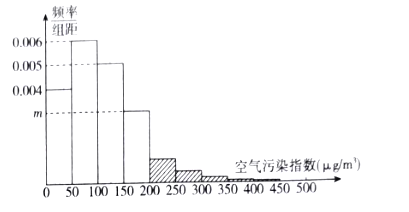
(I)求頻率分布直方圖中![]() 的值(寫出推理過程,直接寫出答案不得分);
的值(寫出推理過程,直接寫出答案不得分);
(II)若按分層抽樣的方法,從空氣質量良好與中度污染的天氣中抽取6天,再從這6天中隨機抽取2天,求至少有一天空氣質量中度污染的概率;
(III)該市環保局為了調查汽車尾氣排放對空氣質量的影響,對限行兩年來的11月份共60天的空氣質量進行統計,其結果如下表:

根據限行前6年180天與限行后60天的數據,計算并填寫以下![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為空氣質量的優良與汽車尾氣的排放有關.
的把握認為空氣質量的優良與汽車尾氣的排放有關.

參考數據:

參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“雙十二”是繼“雙十一”之后的又一個網購狂歡節,為了刺激“雙十二”的消費,某電子商務公司決定對“雙十一”的網購者發放電子優惠券.為此,公司從“雙十一”的網購消費者中用隨機抽樣的方法抽取了100人,將其購物金額(單位:萬元)按照![]() ,
, ![]() 分組,得到如下頻率分布直方圖:
分組,得到如下頻率分布直方圖:
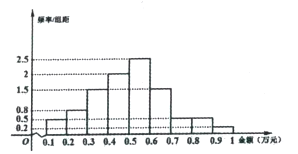
根據調查,該電子商務公司制定了發放電子優惠券的辦法如下:

(Ⅰ)求購物者獲得電子優惠券金額的平均數;
(Ⅱ)從這100名購物金額不少于0.8萬元的人中任取2人,求這兩人的購物金額在0.8~0.9萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家電公司根據銷售區域將銷售員分成![]() ,
,![]() 兩組.
兩組.![]() 年年初,公司根據銷售員的銷售業績分發年終獎,銷售員的銷售額(單位:十萬元)在區間
年年初,公司根據銷售員的銷售業績分發年終獎,銷售員的銷售額(單位:十萬元)在區間![]() ,
,![]() ,
,![]() ,
,![]() 內對應的年終獎分別為2萬元,2.5萬元,3萬元,3.5萬元.已知銷售員的年銷售額都在區間
內對應的年終獎分別為2萬元,2.5萬元,3萬元,3.5萬元.已知銷售員的年銷售額都在區間![]() 內,將這些數據分成4組:
內,將這些數據分成4組:![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下兩個頻率分布直方圖:
,得到如下兩個頻率分布直方圖:
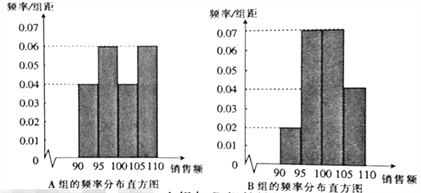
以上面數據的頻率作為概率,分別從![]() 組與
組與![]() 組的銷售員中隨機選取1位,記
組的銷售員中隨機選取1位,記![]() ,
,![]() 分別表示
分別表示![]() 組與
組與![]() 組被選取的銷售員獲得的年終獎.
組被選取的銷售員獲得的年終獎.
(1)求![]() 的分布列及數學期望;
的分布列及數學期望;
(2)試問![]() 組與
組與![]() 組哪個組銷售員獲得的年終獎的平均值更高?為什么?
組哪個組銷售員獲得的年終獎的平均值更高?為什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】暑假期間,某旅行社為吸引游客去某風景區旅游,推出如下收費標準:若旅行團人數不超過30,則每位游客需交費用600元;若旅行團人數超過30,則游客每多1人,每人交費額減少10元,直到達到70人為止.
(1)寫出旅行團每人需交費用![]() (單位:元)與旅行團人數
(單位:元)與旅行團人數![]() 之間的函數關系式;
之間的函數關系式;
(2)旅行團人數為多少時,旅行社可以從該旅行團獲得最大收入?最大收入是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com