
已知二次函數 (其中
(其中 )
)
(1)試討論函數 的奇偶性.
的奇偶性.
(2)當 為偶函數時,若函數
為偶函數時,若函數 ,
,
試證明:函數 在
在 上單調遞減,在
上單調遞減,在 上單調遞增;
上單調遞增;
(1) 函數
函數 是非奇非偶函數
是非奇非偶函數
(2)見解析
【解析】本試題主要是考查了二次函數的性質,以及函數奇偶性和單調性的綜合運用。
(1)函數 的定義域為R關于原點對稱,………
的定義域為R關于原點對稱,……… 
 故此時函數
故此時函數 是偶函數
是偶函數


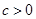 ,
, 故函數
故函數 不是奇函數,且易知此時
不是奇函數,且易知此時 故函數
故函數 也不是偶函數,所以
也不是偶函數,所以 函數
函數 是非奇非偶函數
是非奇非偶函數
(2)
 為偶函數,由(1)知
為偶函數,由(1)知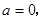
 利用定義法判定單調性。
利用定義法判定單調性。
解:(1) 函數 的定義域為R關于原點對稱,………. 1分
的定義域為R關于原點對稱,………. 1分

 故此時函數
故此時函數 是偶函數……….2分
是偶函數……….2分


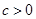 ,
, 故函數
故函數 不是奇函數,且易知此時
不是奇函數,且易知此時 故函數
故函數 也不是偶函數,所以
也不是偶函數,所以 函數
函數 是非奇非偶函數……….4分
是非奇非偶函數……….4分
(其他合理方式解答相應給分)
(2)
 為偶函數,由(1)知
為偶函數,由(1)知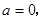
 ……….5分
……….5分
 ,則
,則 ……….7分
……….7分
=
 ……………9分
……………9分

 ,則
,則 <0
<0
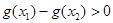 ,
, 
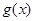 在
在 上單調遞減, ……….11分
上單調遞減, ……….11分
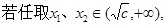
 ,則
,則 >0
>0
 <0 ,
<0 , 
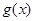 在
在 上單調遞增, ……….13分
上單調遞增, ……….13分


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數學 來源:2010-2011年廣東省廣州市高一下學期期末考試數學 題型:解答題
(本小題滿分14分)
已知二次函數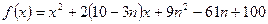 ,其中
,其中 .
.
(1)設函數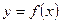 的圖象的頂點的橫坐標
的圖象的頂點的橫坐標 構成數列
構成數列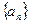 ,求證:數列
,求證:數列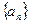 為等差數
為等差數 列;
列;
(2)設函數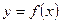 的圖象的頂點到
的圖象的頂點到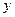 軸的距離構成數列
軸的距離構成數列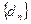 ,求數列
,求數列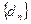 的前
的前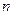 項和
項和 .
.
查看答案和解析>>
科目:高中數學 來源:2015屆廣東省高一上學期期中考試數學試卷(解析版) 題型:解答題
本小題滿分10分
已知二次函數 (其中
(其中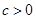 ).
).
(1)若函數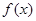 為偶函數,求
為偶函數,求 的值;
的值;
(2)當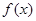 為偶函數時,若函數
為偶函數時,若函數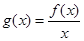 ,指出
,指出 在
在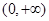 上單調性情況,并證明之.
上單調性情況,并證明之.
查看答案和解析>>
科目:高中數學 來源:2010-2011年廣東省廣州市高一下學期期末考試數學 題型:解答題
(本小題滿分14分)
已知二次函數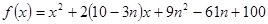 ,其中
,其中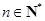 .
.
(1)設函數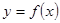 的圖象的頂點的橫坐標構成數列
的圖象的頂點的橫坐標構成數列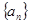 ,求證:數列
,求證:數列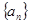 為等差數列;
為等差數列;
(2)設函數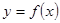 的圖象的頂點到
的圖象的頂點到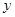 軸的距離構成數列
軸的距離構成數列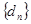 ,求數列
,求數列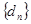 的前
的前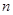 項和
項和 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com