
如圖,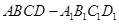 是棱長為1的正方體,四棱錐
是棱長為1的正方體,四棱錐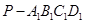 中,
中,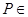 平面
平面 ,
,
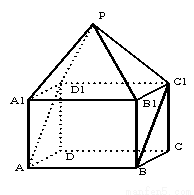
(Ⅰ)求證: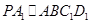
(Ⅱ)求直線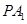 與平面
與平面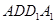 所成角的正切值。
所成角的正切值。
(1)利用線面平行的判定定理來證明。(2)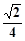
【解析】
試題分析:(Ⅰ)取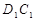 的中點
的中點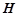 ,連結
,連結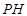 ,
,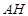 .
.
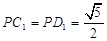 ,
,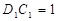 ,
,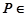 平面
平面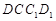 ,
,
∴ ,
,
∴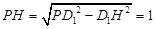 ,
,
∴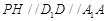 ,
, 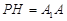 ,
,
∴四邊形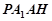 為平行四邊形,
為平行四邊形,
∴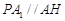 ,
,
又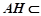 平面
平面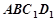 ,
,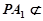 平面
平面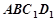 ,∴
,∴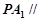 平面
平面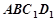 .
.
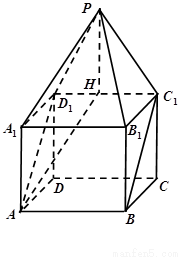
(Ⅱ)∵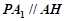 ,
,
∴直線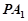 與平面
與平面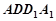 所成角等于直線
所成角等于直線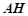 與平面
與平面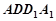 所成角.
所成角.
正方體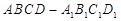 中,顯然
中,顯然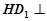 平面
平面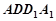 ,
,
∴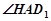 就是直線
就是直線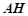 與平面
與平面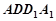 所成角.
所成角.
在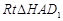 中,
中,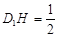 ,
,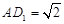 ,
,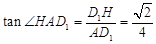
∴直線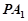 與平面
與平面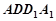 所成角的正切值為
所成角的正切值為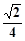 .
.
考點:本試題考查了線面平行的證明以及線面角的求解。
點評:解決立體幾何中的平行和垂直的證明一般都要根據所學的線面和面面的平行和垂直的判定定理和性質定理來得到。同時能利用平面的垂線來得到斜線在平面內的射影,進而得到線面角,結合三角形來求解,屬于中檔題。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
 如圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點,O是點A在平面BCD內的射影.
如圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點,O是點A在平面BCD內的射影.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
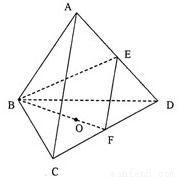
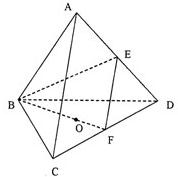 如圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點,O是點A在平面BCD內的射影.
如圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點,O是點A在平面BCD內的射影.查看答案和解析>>
科目:高中數學 來源: 題型:
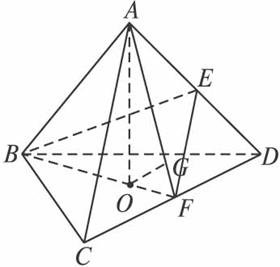
(1)求直線EF與直線BC所成角的大小;
(2)求點O到平面ACD的距離;
(3)(理)求二面角ABEF的大小.
(文)求二面角CBFE的大小.
查看答案和解析>>
科目:高中數學 來源:2007年北京市朝陽區高考數學一模試卷(理科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2009-2010學年度新課標高二下學期數學單元測試1-理科 題型:解答題
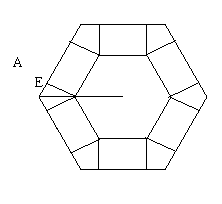
如圖,把邊長為a的正六邊形紙板剪去相同的六個角,做成一個底面為正六邊形的無蓋六棱柱盒子,設高為h所做成的盒子體積V(不計接縫).
(1)寫出體積V與高h的函數關系式;
 (2)當
(2)當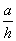 為多少時,體積V最大,最大值是多少?
為多少時,體積V最大,最大值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com