
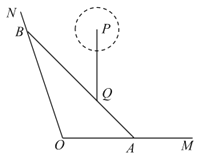
【題目】如圖,![]() ,
,![]() 是某景區的兩條道路(寬度忽略不計,
是某景區的兩條道路(寬度忽略不計,![]() 為東西方向),Q為景區內一景點,A為道路
為東西方向),Q為景區內一景點,A為道路![]() 上一游客休息區,已知
上一游客休息區,已知![]() ,
,![]() (百米),Q到直線
(百米),Q到直線![]() ,
,![]() 的距離分別為3(百米),
的距離分別為3(百米),![]() (百米),現新修一條自A經過Q的有軌觀光直路并延伸至道路
(百米),現新修一條自A經過Q的有軌觀光直路并延伸至道路![]() 于點B,并在B處修建一游客休息區.
于點B,并在B處修建一游客休息區.
(1)求有軌觀光直路![]() 的長;
的長;
(2)已知在景點Q的正北方6百米的P處有一大型組合音樂噴泉,噴泉表演一次的時長為9分鐘,表演時,噴泉噴灑區域以P為圓心,r為半徑變化,且t分鐘時,![]() (百米)(
(百米)(![]() ,
,![]() ).當噴泉表演開始時,一觀光車S(大小忽略不計)正從休息區B沿(1)中的軌道
).當噴泉表演開始時,一觀光車S(大小忽略不計)正從休息區B沿(1)中的軌道![]() 以
以![]() (百米/分鐘)的速度開往休息區A,問:觀光車在行駛途中是否會被噴泉噴灑到,并說明理由.
(百米/分鐘)的速度開往休息區A,問:觀光車在行駛途中是否會被噴泉噴灑到,并說明理由.
【答案】(1)![]() ;(2)噴泉的水流不會灑到觀光車上,理由見解析
;(2)噴泉的水流不會灑到觀光車上,理由見解析
【解析】
(1)建立如圖平面直角坐標系,易得![]() ,直線
,直線![]() 的方程為
的方程為![]() ,
,![]()
![]() ,由點到直線距離,求出
,由點到直線距離,求出![]() ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯產方程組求出
,聯產方程組求出![]() 的坐標,由此能求出軌道的長;
的坐標,由此能求出軌道的長;
(2)將噴泉記為圓![]() ,由題意得
,由題意得![]() ,生成
,生成![]() 分鐘時,觀光車在線段AB上的點C處,則
分鐘時,觀光車在線段AB上的點C處,則![]() ,
,![]() ,從而
,從而![]() ,若噴泉不會灑到觀光車上,則
,若噴泉不會灑到觀光車上,則![]() 對
對![]() 恒成立,由此能求出噴泉的水流不會灑到觀光車上.
恒成立,由此能求出噴泉的水流不會灑到觀光車上.
(1)以點O為坐標原點,直線![]() 為x軸,建立平面直角坐標系,如圖所示.
為x軸,建立平面直角坐標系,如圖所示.
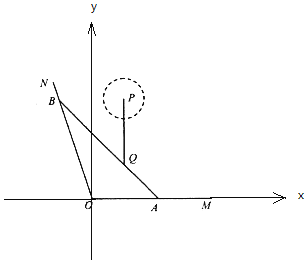
則由題設得:![]() ,直線
,直線![]() 的方程為
的方程為![]() ,
,![]() (
(![]() ).
).
由![]() ,解得
,解得![]() ,所以
,所以![]() .
.
故直線![]() 的方程為
的方程為![]() ,
,
由![]() 得
得![]()
即![]() ,故
,故![]() ,
,
答:水上旅游線![]() 的長為
的長為![]() .
.
(2)將噴泉記為圓P,由題意可得![]() ,
,
生成t分鐘時,觀光車在線段![]() 上的點C處,
上的點C處,
則![]() ,
,![]() ,所以
,所以![]() .
.
若噴泉不會灑到觀光車上,則![]() 對
對![]() 恒成立,
恒成立,
即![]() ,
,
當![]() 時,上式成立,
時,上式成立,
當![]() 時,
時,![]() ,
,![]() ,當且僅當
,當且僅當![]() 時取等號,
時取等號,
因為![]() ,所以
,所以![]() 恒成立,即噴泉的水流不會灑到觀光車上.
恒成立,即噴泉的水流不會灑到觀光車上.
答:噴泉的水流不會灑到觀光車上.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】橢圓![]() (
(![]() )的離心率是
)的離心率是![]() ,點
,點![]() 在短軸
在短軸![]() 上,且
上,且![]() 。
。
(1)球橢圓![]() 的方程;
的方程;
(2)設![]() 為坐標原點,過點
為坐標原點,過點![]() 的動直線與橢圓交于
的動直線與橢圓交于![]() 兩點。是否存在常數
兩點。是否存在常數![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線![]() ax+by=1與圓x2+y2=1相交于A,B兩點(其中a,b是實數),且△AOB是直角三角形(O是坐標原點),則點P(a,b)與點(0,1)之間距離的最小值為( ).
ax+by=1與圓x2+y2=1相交于A,B兩點(其中a,b是實數),且△AOB是直角三角形(O是坐標原點),則點P(a,b)與點(0,1)之間距離的最小值為( ).
A.0B.![]() C.
C.![]() -1D.
-1D.![]() +1
+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數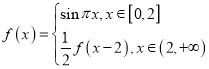 ,有下列說法:
,有下列說法:
①函數![]() 對任意
對任意![]() ,都有
,都有![]() 成立;
成立;
②函數![]() 在
在![]() 上單調遞減;
上單調遞減;
③函數![]() 在
在![]() 上有3個零點;
上有3個零點;
④若函數![]() 的值域為
的值域為![]() ,設
,設![]() 是
是![]() 中所有有理數的集合,若簡分數
中所有有理數的集合,若簡分數![]() (其中
(其中![]() ,
,![]() 為互質的整數),定義函數
為互質的整數),定義函數![]() ,則
,則![]() 在
在![]() 中根的個數為5;
中根的個數為5;
其中正確的序號是______(填寫所有正確結論的番號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com