
在如圖所示的幾何體中, 是邊長為
是邊長為 的正三角形,
的正三角形, ,
, 平面
平面 ,平面
,平面 平面
平面 ,
,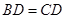 ,且
,且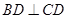 .
.
(1)證明: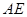 //平面
//平面 ;
;
(2)證明:平面 平面
平面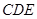 ;
;
(3)求該幾何體的體積.
(1)詳見解析;(2)詳見解析;(3)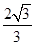
解析試題分析:(1)取 的中點
的中點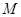 ,根據等腰三角形中線即為高線可得
,根據等腰三角形中線即為高線可得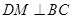 ,又因為面
,又因為面 平面
平面 ,根據面面垂直的性質定理可得
,根據面面垂直的性質定理可得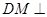 平面
平面 ,已知
,已知 平面
平面 ,所以
,所以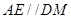 ,根據線面平行的判定定理可得
,根據線面平行的判定定理可得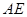 //平面
//平面 。(2)因為
。(2)因為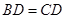 ,且
,且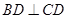 ,斜邊中線
,斜邊中線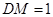 ,又因為
,又因為 ,
,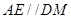 可證得
可證得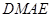 是平行四邊形,可得
是平行四邊形,可得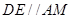 ,根據線面垂直的判定定理可證得
,根據線面垂直的判定定理可證得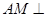 平面
平面 ,即
,即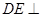 平面
平面 ,從而可得
,從而可得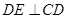 ,又因為
,又因為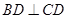 即可證得
即可證得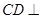 平面
平面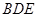 ,從而證得平面
,從而證得平面 平面
平面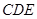 。(3)根據前兩問的條件可證得
。(3)根據前兩問的條件可證得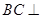 平面
平面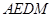 ,從而可將此幾何體分割為以四邊形
,從而可將此幾何體分割為以四邊形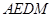 為底面的兩個四棱錐,然后再求其體積。
為底面的兩個四棱錐,然后再求其體積。
試題解析:證明:
(1) 取 的中點
的中點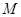 ,連接
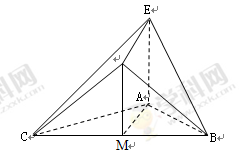
,連接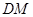 、
、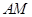 ,
,
由已知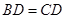 ,可得:
,可得: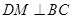 ,
,
又因為平面 ⊥平面
⊥平面 ,平面
,平面
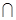 平面
平面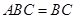 ,
,
所以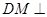 平面
平面 ,
,
因為 平面
平面 , 所以
, 所以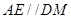 ,
,
又因為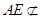 平面
平面 ,
,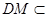 平面
平面 ,
,
所以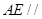 平面
平面 . 4分
. 4分
(2)由(1)知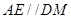 ,又
,又 ,
,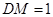 ,
,
所以四邊形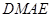 是平行四邊形,則有
是平行四邊形,則有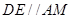 ,
,
由(1)得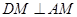 ,又
,又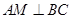 ,
,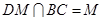
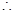
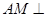 平面
平面 , 所以
, 所以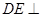 平面
平面 ,
,
又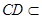


科目:高中數學 來源: 題型:解答題
如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,四邊形ABCD是菱形,AC=6,BD=8,E是PB上任意一點,△AEC面積的最小值是3.
(1)求證:AC⊥DE;
(2)求四棱錐P-ABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖所示,矩形ABCD中,AB=a,AD=b,過點D作DE⊥AC于E,交直線AB于F.現將△ACD沿對角線AC折起到△PAC的位置,使二面角P AC
AC B的大小為60°.過P作PH⊥EF于H.
B的大小為60°.過P作PH⊥EF于H.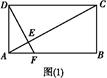
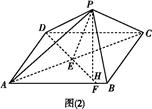
(1)求證:PH⊥平面ABC;
(2)若a+b=2,求四面體P ABC體積的最大值.
ABC體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖甲,⊙O的直徑AB=2,圓上兩點C、D在直徑AB的兩側,且∠CAB=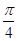 ,∠DAB=
,∠DAB=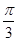 .沿直徑AB折起,使兩個半圓所在的平面互相垂直(如圖乙),F為BC的中點,E為AO的中點.根據圖乙解答下列各題:
.沿直徑AB折起,使兩個半圓所在的平面互相垂直(如圖乙),F為BC的中點,E為AO的中點.根據圖乙解答下列各題: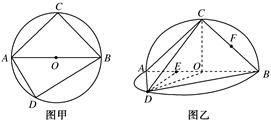
(1)求三棱錐C-BOD的體積;
(2)求證:CB⊥DE;
(3)在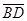 上是否存在一點G,使得FG∥平面ACD?若存在,試確定點G的位置;若不存在,請說明理由.
上是否存在一點G,使得FG∥平面ACD?若存在,試確定點G的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱錐S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,側棱SA 底面ABCD,且SA=2,AD=DC=1, 點E在SD上,且
底面ABCD,且SA=2,AD=DC=1, 點E在SD上,且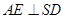
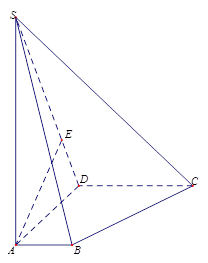
(1)證明: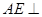 平面
平面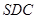 ;
;
(2)求三棱錐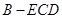 的體積
的體積
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱錐P-ABCD中,側棱PA⊥底面ABCD,底面ABCD為矩形,E為PD上一點,AD=2AB=2AP=2,PE=2DE.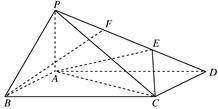
(1)若F為PE的中點,求證:BF∥平面ACE;
(2)求三棱錐P-ACE的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com