【題目】已知
.
（1）求函數
最值；
（2）若
，求證：
.
【答案】（1） 
取最大值
，無最小值；（2）詳見解析.
【解析】
試題分析：（1）分析函數的導數，并且求函數的極值點，并且分析極值點兩側的單調性，求函數的最值；
（2）設
，根據（1）可知
，然后采用分析法的證明思路，轉化為證明
，設
，
，根據函數的導數，可知函數是單調遞增函數，所以
，得證.
試題解析：（1）對求導可得
，
令
得x=0.
當
時，
，函數單調遞增；
當
時，
，函數單調遞減，
當x=0時，取最大值，無最小值.
（2）不妨設，由（1）得
當
時，
，函數單調遞增；
當
時，
，函數單調遞減，
若
，則
，
欲證：
，只需證：
，
∵
函數在單調遞減，
只需證：
，考慮到
，即證
，也即證
下證：
，
設
，
，
∴
，故g（x）在
上單調遞增，
故時，g（x）<g（0）=0，即f（x）-f（-x）<0，∴
.
開心蛙口算題卡系列答案科目：高中數學 來源： 題型：
【題目】某城市要建成宜商、宜居的國際化現代新城，該城市的東城區、西城區分別引進8甲廠家，現對兩個區域的16個廠家進行評估，綜合得分情況如莖葉圖所示.
（1）根據莖葉圖判斷哪個區域廠家的平均分較高；
（2）規定85分以上（含85分）為優秀廠家，若從該兩個區域各選一個優秀廠家，求得分差距不超過5分的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨機抽取某中學高一級學生的一次數學統測成績得到一樣本，其分組區間和頻數是：
，2；
，7；
，10；
，x；[90，100]，2.其頻率分布直方圖受到破壞，可見部分如下圖所示，據此解答如下問題.
（1）求樣本的人數及x的值；
（2）估計樣本的眾數，并計算頻率分布直方圖中
的矩形的高；
（3）從成績不低于80分的樣本中隨機選取2人，該2人中成績在90分以上（含90分）的人數記為
，求的數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了比較兩種治療失眠癥的藥(分別稱為A藥，B藥)的療效，隨機地選取20位患者服用A藥，20位患者服用B藥，這40位患者在服用一段時間后，記錄他們日平均增加的睡眠時間(單位：h)．試驗的觀測結果如下：
服用A藥的20位患者日平均增加的睡眠時間：
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B藥的20位患者日平均增加的睡眠時間：
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分別計算兩組數據的平均數，從計算結果看，哪種藥的療效更好？
(2)根據兩組數據繪制莖葉圖，從莖葉圖看，哪種藥的療效更好？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
有如下性質：如果常數
，那么該函數在
上是減函數，在
上是增函數．
（1）已知
，利用上述性質，求函數
的單調區間和值域；
（2）對于（1）中的函數
和函數
，若對任意
，總存在
，使得
成立，求實數
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖（1）,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
AP=2,D是AP的中點,E,F,G分別是PC,PD,CB的中點,將△PCD沿CD折起,使點P在平面ABCD內的射影為點D,如圖（2）．
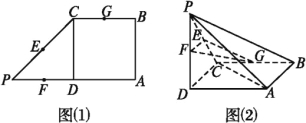
（1）求證:AP∥平面EFG;
（2）求三棱錐P-ABC的體積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
