【題目】
不是直角三角形，它的三個角
所對的邊分別為
，已知
.
（1）求證： 
；
（2）如果
，求
面積的最大值.
【答案】（1）見解析；（2）48
【解析】試題分析：（1）由
，根據正弦定理及兩角和的正弦公式化簡可得
，因為
不是直角三角形，所以
，由正弦定理可得
；（2）視
為定點,求出滿足
條件下
的軌跡為一個圓，圓心在直
上，當
上升到離直線
最遠時面積最大.
試題解析：（1）由
，根據正弦定理可得
， 
，因為
不是直角三角形，所以
，由正弦定理可得
；
（2）方法一：b=2a.c=12，余弦定理用a表示cosC,表示出sinC,進而用a表示出
,求出該函數的最大值.(最費力的做法)
方法二:視A.B為定點,求出滿足b=2a條件下C的軌跡為一個圓，圓心在直線AB上，當C上升到離直線AB最遠時面積最大。
方法三：利用海倫公式直接將面積表示為a的函數
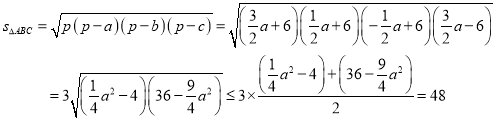
方法三為最簡捷辦法，凡只涉及邊的面積問題可優先想到海倫公式。
暑假作業海燕出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓C：
的離心率為
，點P（1，）在橢圓C上，直線l過橢圓的右焦點與橢圓相交于A，B兩點．
（1）求橢圓C的方程；
（2）在x軸上是否存在定點M，使得
為定值？若存在，求定點M的坐標；若不在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對在直角坐標系的第一象限內的任意兩點
，
作如下定義:
,那么稱點是點的“上位點”，同時點是點的“下位點”.
（1）試寫出點
的一個“上位點”坐標和一個“下位點”坐標；
（2）設
、
、
、
均為正數，且點是點的上位點，請判斷點
是否既是點的“下位點”又是點的“上位點”，如果是請證明，如果不是請說明理由；
（3）設正整數
滿足以下條件：對任意實數
，總存在
，使得點
既是點
的“下位點”，又是點
的“上位點”，求正整數的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
按照某學者的理論，假設一個人生產某產品單件成本為
元，如果他賣出該產品的單價為
元，則他的滿意度為
；如果他買進該產品的單價為
元，則他的滿意度為
.如果一個人對兩種交易(賣出或買進)的滿意度分別為
和
，則他對這兩種交易的綜合滿意度為
.
現假設甲生產A、B兩種產品的單件成本分別為12元和5元，乙生產A、B兩種產品的單件成本分別為3元和20元，設產品A、B的單價分別為
元和
元，甲買進A與賣出B的綜合滿意度為
，乙賣出A與買進B的綜合滿意度為
(1)求和關于、的表達式；當
時，求證：=；
(2)設，當、分別為多少時，甲、乙兩人的綜合滿意度均最大？最大的綜合滿意度為多少？(3)記(2)中最大的綜合滿意度為
，試問能否適當選取、的值，使得
和
同時成立，但等號不同時成立？試說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C中心在原點，焦點在x軸上，左右焦點分別為F1，F2，且|F1F2|=2，點（1，
）在橢圓C上．
（1）求橢圓C的方程；
（2）過F1的直線l與橢圓C相交于A，B兩點，且△AF2B的面積為
，求以F2為圓心且與直線l相切的圓的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
. 
為實數，且
，記由所有
組成的數集為
.
（1）已知
，求
；
（2）對任意的
，
恒成立，求的取值范圍；
（3）若
，
，判斷數集中是否存在最大的項？若存在，求出最大項；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，圓C的參數方程
（φ為參數）．以O為極點，x軸的非負半軸為極軸建立極坐標系．
（Ⅰ）求圓C的極坐標方程；
（Ⅱ）直線l的極坐標方程是ρ（sinθ+
）=3
，射線OM：θ=
與圓C的交點為O，P，與直線l的交點為Q，求線段PQ的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，從參加環保知識競賽的學生中抽出
名，將其成績（均為整數）整理后畫出的頻率分布直方圖如下：觀察圖形，回答下列問題：
（1）
這一組的頻數、頻率分別是多少？
（2）估計這次環保知識競賽成績的平均數、眾數、中位數。（不要求寫過程）
(3) 從成績是80分以上（包括80分）的學生中選兩人，求他們在同一分數段的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
