
設函數f(x)=ax2+bx+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的零點;
(2)若對任意b∈R,函數f(x)恒有兩個不同零點,求實數a的取值范圍.
 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源: 題型:解答題
(13分)某工廠某種產品的年固定成本為250萬元,每生產x千件,需另投入成本C(x),當年產量不足80千件時,C(x)= x2+10x(萬元);當年產量不小于80千件時,C(x)=51x+
x2+10x(萬元);當年產量不小于80千件時,C(x)=51x+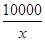 -1 450(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
-1 450(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤L(x)(萬元)關于年產量x(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于定義域為A的函數f(x),如果任意的x1,x2∈A,當x1<x2時,都有f(x1)<f(x2),則稱函數f(x)是A上的嚴格增函數;函數f(k)是定義在N*上,函數值也在N*中的嚴格增函數,并且滿足條件f(f(k))=3k.
(1)證明:f(3k)=3f(k);
(2)求f(3k-1)(k∈N*)的值;
(3)是否存在p個連續的自然數,使得它們的函數值依次也是連續的自然數;若存在,找出所有的p值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=ax2+bx+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的零點;
(2)若對任意b∈R,函數f(x)恒有兩個不同零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=ax2+bx+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的零點;
(2)若對任意b∈R,函數f(x)恒有兩個不同零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位擬建一個扇環面形狀的花壇(如圖所示),該扇環面是由以點 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點 的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為 米,圓心角為
米,圓心角為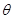 (弧度).
(弧度).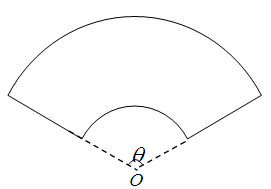
(1)求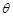 關于
關于 的函數關系式;
的函數關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為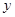 ,求
,求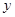 關于
關于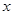 的函數關系式,并求出
的函數關系式,并求出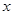 為何值時,
為何值時,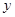 取得最大值?
取得最大值?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com