
已知橢圓E:![]() 的一個交點為
的一個交點為![]() ,而且過點
,而且過點![]() .
.
(Ⅰ)求橢圓E的方程;
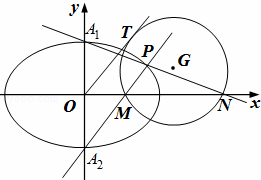
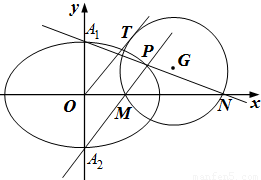
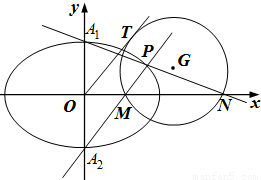
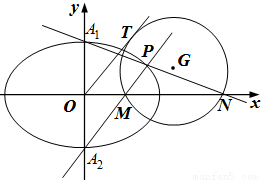
(Ⅱ)設橢圓E的上下頂點分別為A1,A2,P是橢圓上異于A1,A2的任一點,直線PA1,PA2分別交x軸于點N,M,若直線OT與過點M,N的圓G相切,切點為T.證明:線段OT的長為定值,并求出該定值.
考點:
圓與圓錐曲線的綜合;橢圓的定義;橢圓的標準方程.
分析:
(Ⅰ)解法一:根據橢圓E:![]() 的一個交點為
的一個交點為![]() ,過點
,過點![]() ,可得a2﹣b2=3,
,可得a2﹣b2=3,![]() ,聯立即可求得橢圓E的方程;
,聯立即可求得橢圓E的方程;
解法二:橢圓的兩個焦點分別為![]() ,利用橢圓的定義,可求橢圓E的方程;
,利用橢圓的定義,可求橢圓E的方程;
(Ⅱ)解法一:由(Ⅰ)可知A1(0,1),A2(0,﹣1),設P(x0,y0),求出![]() ,同
,同![]()
設圓G的圓心為![]() ,利用
,利用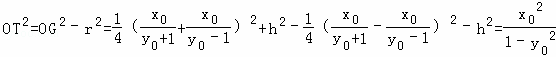 ,即可得到線段OT的長度;
,即可得到線段OT的長度;
解法二:由(Ⅰ)可知A1(0,1),A2(0,﹣1),設P(x0,y0),求出![]() ,
,![]() ,可得
,可得 ,由切割線定理可得線段OT的長度.
,由切割線定理可得線段OT的長度.
解答:
(Ⅰ)解法一:由題意,∵橢圓E:![]() 的一個交點為
的一個交點為![]() ,
,
∴a2﹣b2=3,①
∵橢圓過點![]() .
.
∴![]() ,②
,②
①②解得a2=4,b2=1,
所以橢圓E的方程為![]() .…(4分)
.…(4分)
解法二:橢圓的兩個焦點分別為![]() ,
,
由橢圓的定義可得![]() ,所以a=2,b2=1,
,所以a=2,b2=1,
所以橢圓E的方程為![]() .…(4分)
.…(4分)
(Ⅱ)解法一:由(Ⅰ)可知A1(0,1),A2(0,﹣1),設P(x0,y0),
直線PA1:![]() ,令y=0,得
,令y=0,得![]() ;
;
直線PA2:![]() ,令y=0,得
,令y=0,得![]() ;
;
設圓G的圓心為![]() ,
,
則r2=![]() ,
,
![]()
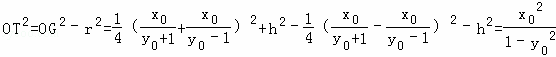
而![]() ,所以
,所以![]() ,所以
,所以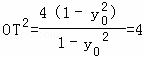 ,
,
所以|OT|=2,即線段OT的長度為定值2.…(14分)
解法二:由(Ⅰ)可知A1(0,1),A2(0,﹣1),設P(x0,y0),
直線PA1:![]() ,令y=0,得
,令y=0,得![]() ;
;
直線PA2:![]() ,令y=0,得
,令y=0,得![]() ;
;
則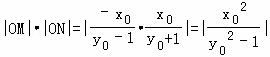 ,而
,而![]() ,所以
,所以![]() ,
,
所以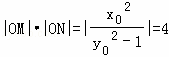 ,由切割線定理得OT2=|OM|•|ON|=4
,由切割線定理得OT2=|OM|•|ON|=4
所以|OT|=2,即線段OT的長度為定值2.…(14分)
點評:
本題考查橢圓的標準方程,考查圓與橢圓為綜合,考查線段長的求解,認真審題,挖掘隱含是關鍵.


 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:解答題
 已知橢圓E:
已知橢圓E: 的一個交點為
的一個交點為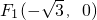 ,而且過點
,而且過點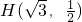 .
.查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北省武漢市高三(上)11月調考數學試卷(理科)(解析版) 題型:解答題
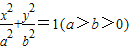 的一個交點為
的一個交點為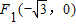 ,而且過點
,而且過點 .
.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北省武漢市高三(上)11月調考數學試卷(文科)(解析版) 題型:解答題
 的一個交點為
的一個交點為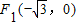 ,而且過點
,而且過點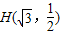 .
.
查看答案和解析>>
科目:高中數學 來源:2013年廣東省高考數學模擬最后一卷(文科)(解析版) 題型:解答題
 的一個交點為
的一個交點為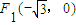 ,而且過點
,而且過點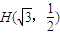 .
.
查看答案和解析>>
科目:高中數學 來源:2012年廣東省佛山市高考數學二模試卷(理科)(解析版) 題型:解答題
 的一個交點為
的一個交點為 ,而且過點
,而且過點 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com