
(2)已知矩形ABCD中,點C坐標為(4,4),A點在曲線x2+y2=9(x>0,y>0)上移動,且AB、AD兩邊始終分別平行于x、y坐標軸,求矩形ABCD面積最小時點A的坐標.
解:(1)設內接矩形在第一象限內的頂點為P(acosθ,bsinθ),則有S內接矩形=4S矩形AOBP=4·acosθ·bsinθ=2absin2θ.
∵θ∈[0,![]() ],
],
∴2θ∈[0,π].
∴S內接矩形的最大值為2ab.
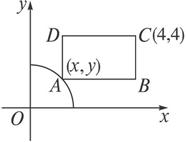
(2)如圖所示,設A(x,y),又設矩形ABCD的面積為S,則有S=(4-x)(4-y)=16-4(x+y)+xy.
∵A(x,y)在曲線x2+y2=9上,
∴x2+y2=(x+y)2-2xy=9.
∴xy=![]() .
.
∴S=16-4(x+y)+![]() =
=![]() [(x+y)-4]2+
[(x+y)-4]2+![]() .
.
又∵x=3cosθ,y=3sinθ(0<θ<![]() ),
),
∴x+y=3(cosθ+sinθ)=![]() sin(θ+
sin(θ+![]() ).
).
∵![]() <θ+
<θ+![]() <
<![]() ,∴3<x+y≤
,∴3<x+y≤![]() .
.
∴當x+y=4時,S有最小值.
解方程組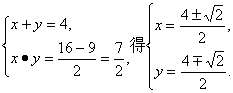
∴A點坐標為(![]() )或(
)或(![]() ).
).


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:高中數學 來源: 題型:
 如圖所示,橢圓C:
如圖所示,橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| OB |
| F1B |
| |F1F2 |
| F1B |
| |F1F2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知橢圓C:
已知橢圓C:| x2 |
| a2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(2)已知矩形ABCD中,點C坐標為(4,4),A點在曲線x2+y2=9(x>0,y>0)上移動,且AB、AD兩邊始終分別平行于x、y坐標軸,求矩形面積ABCD最小時點A的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com