
(1)求b與c的關系式(用c表示b);
(2)設函數F(x)=f(x)g(x)在(-¥,+¥)內有極值點,求c的取值范圍.
| 本小題考查導數、切線、極值等知識及綜合運用數學知識解決問題的能力
解:(1)依題意,令f(x)=g¢(x),得2x+b=1,故x= 由于 ∵ b>-1,c>0,∴ b=-1+ (2)F(x)=f(x)g(x)=x3+2bx2+(b2+c)x+bc. ∴ F¢(x)=3x2+4bx+b2+c.令F¢(x)=0,即3x2+4bx+b2+c=0. 則D=16b2-12(b2+c)=4(b2-3c) 若D=0,則F¢(x)=0有一個實數根x0,且F¢(x)的變化如下:
于是x=x0不是函數F(x)的極值點. 若D>0,則F¢(x)=0有兩個不相等的實根x1、x2(x1<x2),且F¢(x)的變化如下:
由此x=x1是函數F(x)的極大值點,是x=x2函數F(x)的極小值點. 綜上所述,當且僅當D>0時,函數F(x)在(-¥,+¥)上有極值點. 由D=4(b2-3c)>0得b< ∵ b=-1+ 解之得0<c<7- 故所求c的取值范圍是(0,7- |


科目:高中數學 來源: 題型:044
已知b>-1,c>0,函數f(x)=x+b的圖像與函數g(x)=x2+bx+c的圖像相切.
(1)求b與c的關系式(用c表示b);
(2)設函數F(x)=f(x)g(x)在(-¥,+¥)內有極值點,求c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知b>-1,c>0,函數![]() 的圖象與函數
的圖象與函數![]() 的圖象相切.
的圖象相切.
(Ⅰ)設![]()
(Ⅱ)是否存在常數c,使得函數![]() 內有極值點?若存在,求出c的取值范圍;若不存在,請說明理由.
內有極值點?若存在,求出c的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2015屆廣東省高一下學期期末考試數學試卷(解析版) 題型:填空題
已知b>0,直線b2x+y+1=0與ax-(b2+4)y+2=0互相垂直,則ab的最小值為________.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三5月高考沖刺理科數學試卷(解析版) 題型:解答題
已知m>1,直線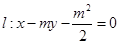 ,橢圓C:
,橢圓C: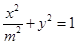 ,
,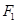 、
、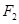 分別為橢圓C的左、右焦點.
分別為橢圓C的左、右焦點.
(Ⅰ)當直線過右焦點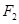 時,求直線的方程;
時,求直線的方程;
(Ⅱ)設直線與橢圓C交于A、B兩點,△A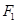
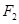 、△B
、△B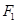
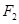 的重心分別為G、H.若原點O在以線段GH為直徑的圓內,求實數m的取值范圍.
的重心分別為G、H.若原點O在以線段GH為直徑的圓內,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com