
【題目】已知y=f(x)是R上的可導函數,對于任意的正實數t,都有函數g(x)=f(x+t)﹣f(x)在其定義域內為減函數,則函數y=f(x)的圖象可能為如圖中( )
A.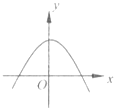
B.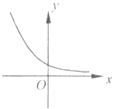
C.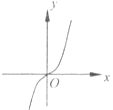
D.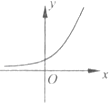
【答案】A
【解析】解:∵函數g(x)=f(x+t)﹣f(x)在其定義域內為減函數, ∴g'(x)=f'(x+t)﹣f'(x)<0在其定義域內恒成立
即f'(x+t)<f'(x),結合t>0,得函數y=f'(x)是其定義域上的減函數.
對于A,可設函數f(x)=ax2+bx+c,(a<0)
∴f'(x)=2ax+b,滿足在其定義域上為減函數;
對于B,可設f(x)=ax , (0<a<1)
∴f'(x)=axlna,在(0,+∞)上是增函數,不符合題意;
對于C,可設f(x)=x3 , 可得f'(x)=3x2在其定義域上不是減函數,故C不正確;
對于D,可設f(x)=ax , (a>1)
∴f'(x)=axlna,在(0,+∞)上是增函數,不符合題意.
故選A


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中常數
,其中常數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)當![]() 時,若函數
時,若函數![]() 有三個不同的零點,求
有三個不同的零點,求![]() 的取值范圍;
的取值范圍;
(3)設定義在![]() 上的函數
上的函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,當
,當![]() 時,若
時,若![]() 在
在![]() 內恒成立,則稱
內恒成立,則稱![]() 為函數
為函數![]() 的“類對稱點”,請你探究當
的“類對稱點”,請你探究當![]() 時,函數
時,函數![]() 是否存在“類對稱點”,若存在,請最少求出一個“類對稱點” 的橫坐標;若不存在,說明理由.
是否存在“類對稱點”,若存在,請最少求出一個“類對稱點” 的橫坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中實數
,其中實數![]() 為常數,
為常數,![]() 為自然對數的底數.
為自然對數的底數.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)當![]() 時,解關于
時,解關于![]() 的不等式
的不等式![]() ;
;
(3)當![]() 時,如果函數
時,如果函數![]() 不存在極值點,求
不存在極值點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在[﹣1,1]上的奇函數,且f(1)=1,若a,b∈[﹣1,1],a+b≠0時,有 ![]() 成立.
成立.
(1)判斷f(x)在[﹣1,1]上的單調性,并證明它;
(2)解不等式f(x2)<f(2x);
(3)若f(x)≤m2﹣2am+1對所有的a∈[﹣1,1]恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=Asin(ωx+φ)在一個周期內的圖象如圖,此函數的解析式為( ) 
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )??
)??
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}為等差數列,其公差為﹣2,且a7是a3與a9的等比中項,Sn為{an}的前n項和,n∈N* , 則S10的值為( )
A.﹣110
B.﹣90
C.90
D.110
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是偶函數.
是偶函數.
(1)求![]() 的值;
的值;
(2)若函數![]() 的圖像與直線
的圖像與直線![]() 沒有交點,求
沒有交點,求![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,是否存在實數
,是否存在實數![]() 使得
使得![]() 最小值為0,若存在,求出
最小值為0,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產一種儀器的元件,由于受生產能力和技術水平等因素的限制,會產生一些次品,根據經驗知道,次品數P(萬件)與日產量x(萬件)之間滿足關系: 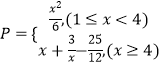 已知每生產l萬件合格的元件可以盈利2萬元,但每生產l萬件次品將虧損1萬元.(利潤=盈利一虧損)
已知每生產l萬件合格的元件可以盈利2萬元,但每生產l萬件次品將虧損1萬元.(利潤=盈利一虧損)
(1)試將該工廠每天生產這種元件所獲得的利潤T(萬元)表示為日產量x(萬件)的函數;
(2)當工廠將這種儀器的元件的日產量x定為多少時獲得的利潤最大,最大利潤為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com