日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

對于平面內(nèi)的命題：“△ABC內(nèi)接于圓O，圓O的半徑為R，且O點在△ABC內(nèi)，連接AO，BO，CO并延長分別交對邊于A1，B1，C1，則AA1+BB1+CC1≥
9R
2
”．
證明如下：
OA1
AA1
+
OB1
BB1
+
OC1
CC1
=
S△OBC
S△ABC
+
S△OAC
S△ABC
+
S△OAB
S△ABC
=1，
即：
AA1-R
AA1
+
BB1-R
BB1
+
CC1-R
CC1
=1，即
1
AA1
+
1
BB1
+
1
CC1
=
2
R
，
由柯西不等式，得(AA1+BB1+CC1)(
1
AA1
+
1
BB1
+
1
CC1
)≥9．∴AA1+BB1+CC1≥
9R
2
．
將平面問題推廣到空間，就得到命題“四面體ABCD內(nèi)接于半徑為R的球O內(nèi)，球心O在該四面體內(nèi)，連接AO，BO，CO，DO并延長分別與對面交于A1，B1，C1，D1，則
AA1+BB1+CC1+DD1≥
16R
3
AA1+BB1+CC1+DD1≥
16R
3
”．
分析：由三角形類比四面體，由面積類比體積，結(jié)合柯西不等式，即可得到結(jié)論．
解答：解：類比證明方法可得：
OA1
AA1
+
OB1
BB1
+
OC1
CC1
+
OD1
DD1
=
VO-DBC
VA-BCD
+
VO-ACD
VA-BCD
+
VO-ABD
VA-BCD
+
VO-ABC
VA-BCD
=1
∴
AA1-R
AA1
+
BB1-R
BB1
+
CC1-R
CC1
+
DD1-R
DD1
=1
∴
1
AA1
+
1
BB1
+
1
CC1
+
1
DD1
=
3
R

由柯西不等式，得(AA1+BB1+CC1+DD1)(
1
AA1
+
1
BB1
+
1
CC1
+
1
DD1
)≥16
∴AA1+BB1+CC1+DD1≥
16R
3

故答案為：AA1+BB1+CC1+DD1≥
16R
3
．
點評：本題考查兩邊推理，考查學(xué)生分析解決問題的能力，考查計算能力，屬于中檔題．
練習(xí)冊系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：

給出下列五個命題：
①長度相等，方向不同的向量叫做相反向量；
②設(shè)
b
，
c
是同一平面內(nèi)的兩個不共線向量，則對于平面內(nèi)的任意一個向量
a
，有且只有一對實數(shù)λ1，λ2，使
a
=λ1
b
+λ2
c
；
③
a
∥
b
的充要條件是存在唯一的實數(shù)λ使
b
=λ
a
；
④（
a
•
b
）
c
=
a
（
b
•
c
）；
⑤λ（
a
+
b
）•
c
=λ
a
•
c
+λ
b
•
c
．
其中正確命題的個數(shù)是                                （　　）

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：湖北省荊州市2012屆高中畢業(yè)班質(zhì)量檢查(Ⅱ)數(shù)學(xué)理科試題 題型：022

對于平面內(nèi)的命題：“△ABC內(nèi)接于圓⊙O，圓O的半徑為R，且O點在△ABC內(nèi)，連結(jié)AO，BO，CO并延長分別交對邊于A1，B1，C1，則AA1＋BB1＋CC1≥”

證明如下：

即：，即

由柯西不等式，得

∴AA1＋BB1＋CC1≥

將平面問題推廣到空間，就得到命題“四面體ABCD內(nèi)接于半徑為R的球O內(nèi)，球心O在該四面體內(nèi)，連結(jié)AO，BO，CO，DO并延長分別與對面交于A1，B1，C1，D1，則________”

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：填空題

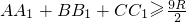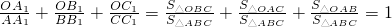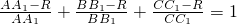對于平面內(nèi)的命題：“△ABC內(nèi)接于圓O，圓O的半徑為R，且O點在△ABC內(nèi)，連接AO，BO，CO并延長分別交對邊于A1，B1，C1，則數(shù)學(xué)公式”．
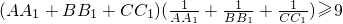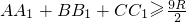證明如下：數(shù)學(xué)公式，
即：數(shù)學(xué)公式，即數(shù)學(xué)公式，
由柯西不等式，得數(shù)學(xué)公式．∴數(shù)學(xué)公式．
將平面問題推廣到空間，就得到命題“四面體ABCD內(nèi)接于半徑為R的球O內(nèi)，球心O在該四面體內(nèi)，連接AO，BO，CO，DO并延長分別與對面交于A1，B1，C1，D1，則________”．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：2011-2012學(xué)年福建省福州三中高三（下）第五次月考數(shù)學(xué)試卷（理科）（解析版） 題型：解答題

對于平面內(nèi)的命題：“△ABC內(nèi)接于圓O，圓O的半徑為R，且O點在△ABC內(nèi)，連接AO，BO，CO并延長分別交對邊于A1，B1，C1，則”．
證明如下：，
即：，即，
由柯西不等式，得．∴．
將平面問題推廣到空間，就得到命題“四面體ABCD內(nèi)接于半徑為R的球O內(nèi)，球心O在該四面體內(nèi)，連接AO，BO，CO，DO并延長分別與對面交于A1，B1，C1，D1，則    ”．

查看答案和解析>>

同步練習(xí)冊答案
主站蜘蛛池模板： 色综合久久久久 | 精品亚洲一区二区三区在线观看 | 国产一区二区三区在线 | 91免费版在线观看 | 成人黄色片网站 | 日韩一区二区精品 | 米奇狠狠狠狠8877 | 亚洲国产一区二区三区四区 | 国产97久久 | 亚洲免费视频网站 | 精品国产精品三级精品av网址 | 久久9久久 | 亚洲欧美电影 | 久免费视频 | 久久亚洲精品中文字幕蜜潮电影 | 国产乱精品一区二区三区视频了 | 国产视频第一页 | 99国产精品久久久久久久成人热 | 精品一区二区视频 | 成人av播放 | 伊人青青久| 欧美日韩视频在线观看免费 | 午夜高清视频 | 青青草一区二区三区 | 国精品一区 | 欧美在线播放一区 | 久久99国产精品 | 欧美亚洲一区 | 国产乱码精品一区二区三区av | 免费观看一级特黄欧美大片 | 精品无码久久久久久国产 | 黄色的网站在线免费观看 | 国产乱码精品一区二区三区忘忧草 | 日本va| 三区在线观看 | 视频在线一区二区 | 欧美国产日韩一区二区三区 | 国内精品国产三级国产在线专 | 天天艹天天干天天 | 成人黄色三级视频 | 日本一级中文字幕久久久久久 |