
【題目】在如圖所示的幾何體中,四邊形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(Ⅰ)求證:BD⊥平面AED;
(Ⅱ)求二面角F﹣BD﹣C的余弦值.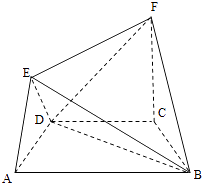
【答案】證明:(I)因為四邊形ABCD是等腰梯形,AB∥CD,∠DAB=60°.所以∠ADC=∠BCD=120°.又CB=CD,
所以∠CDB=30°,因此,∠ADB=90°,AD⊥BD,
又AE⊥BD且,AE∩AD=A,AE,AD平面AED,
所以BD⊥平面AED;
(II)解法一: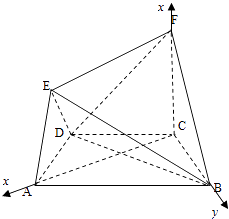
由(I)知,AD⊥BD,同理AC⊥BC,
又FC⊥平面ABCD,因此CA,CB,CF兩兩垂直,以C為坐標原點,分別以CA,CB,CF所在的直線為X軸,Y軸,Z軸建立如圖的空間直角坐標系,
不妨設CB=1,則C(0,0,0),B(0,1,0),D( ![]() ,﹣
,﹣ ![]() ,0),F(0,0,1),因此
,0),F(0,0,1),因此 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,0),
,0), ![]() =(0,﹣1,1)
=(0,﹣1,1)
設平面BDF的一個法向量為 ![]() =(x,y,z),則
=(x,y,z),則 ![]()
![]() =0,
=0, ![]()
![]() =0
=0
所以x= ![]() y=
y= ![]() z,取z=1,則
z,取z=1,則 ![]() =(
=( ![]() ,1,1),
,1,1),
由于 ![]() =(0,0,1)是平面BDC的一個法向量,
=(0,0,1)是平面BDC的一個法向量,
則cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() ,所以二面角F﹣BD﹣C的余弦值為
,所以二面角F﹣BD﹣C的余弦值為 ![]()
解法二: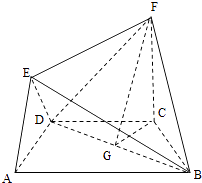
取BD的中點G,連接CG,FG,由于 CB=CD,因此CG⊥BD,又FC⊥平面ABCD,BD平面ABCD,
所以FC⊥BD,由于FC∩CG=C,FC,CG平面FCG.
所以BD⊥平面FCG.故BD⊥FG,所以∠FGC為二面角F﹣BD﹣C的平面角,
在等腰三角形BCD中,由于∠BCD=120°,
因此CG= ![]() CB,又CB=CF,
CB,又CB=CF,
所以GF= ![]() =
= ![]() CG,
CG,
故cos∠FGC= ![]() ,
,
所以二面角F﹣BD﹣C的余弦值為 ![]()
【解析】(Ⅰ)由題意及圖可得,先由條件證得AD⊥BD及AE⊥BD,再由線面垂直的判定定理即可證得線面垂直;(II)解法一:由(I)知,AD⊥BD,可得出AC⊥BC,結合FC⊥平面ABCD,知CA,CA,CF兩兩垂直,因此可以C為坐標原點,分別以CA,CB,CF所在的直線為X軸,Y軸,Z軸建立如圖的空間直角坐標系,設CB=1,表示出各點的坐標,再求出兩個平面的法向量的坐標,由公式求出二面角F﹣BD﹣C的余弦值即可;解法二:取BD的中點G,連接CG,FG,由于 CB=CD,因此CG⊥BD,又FC⊥平面ABCD,BD平面ABCD,可證明出∠FGC為二面角F﹣BD﹣C的平面角,再解三角形求出二面角F﹣BD﹣C的余弦值.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(1+x),g(x)=loga(1+kx),其中a>0且a≠1. (Ⅰ)當k=﹣2時,求函數h(x)=f(x)+g(x)的定義域;
(Ⅱ)若函數H(x)=f(x)﹣g(x)是奇函數(不為常函數),求實數k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐S﹣ABC中,G1 , G2分別是△SAB和△SAC的重心,則直線G1G2與BC的位置關系是( ) 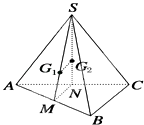
A.相交
B.平行
C.異面
D.以上都有可能
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知以點C(t, ![]() )(t∈R,t≠0)為圓心的圓過原點O.
)(t∈R,t≠0)為圓心的圓過原點O.
(1)設直線3x+y﹣4=0與圓C交于點M,N,若|OM|=|ON|,求圓C的方程;
(2)在(1)的條件下,設B(0,2),且P,Q分別是直線l:x+y+2=0和圓C上的動點,求|PQ|﹣|PB|的最大值及此時點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分別是邊AB,AC上的點,且 ![]() ,
, ![]() ,其中m,n∈(0,1).若EF,BC的中點分別為M,N,且m+4n=1,則
,其中m,n∈(0,1).若EF,BC的中點分別為M,N,且m+4n=1,則 ![]() 的最小值為 .
的最小值為 . 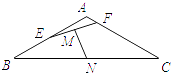
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)為定義在[﹣1,1]上的奇函數,當x∈[﹣1,0]時,函數解析式f(x)= ![]() ﹣
﹣ ![]() (a∈R).
(a∈R).
(1)寫出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com