
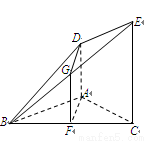
如圖, 平面
平面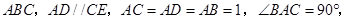 凸多面體
凸多面體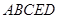 的體積為
的體積為 ,
,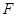 為
為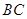 的中點.
的中點.
(Ⅰ)求證: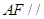 平面
平面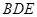 ;
;
(Ⅱ)求證:平面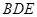
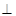 平面
平面 .
.

(Ⅰ)詳見解析;(Ⅱ)詳見解析.
【解析】
試題分析:(Ⅰ)取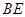 的中點G,連結
的中點G,連結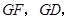 只需證明
只需證明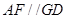 ;(Ⅱ)先證明
;(Ⅱ)先證明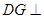 面
面 ,再證平面
,再證平面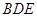
 平面
平面 .
.
試題解析:(Ⅰ)證明: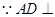 平面
平面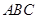 ,
,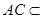 面
面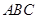 ,
,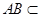 面
面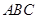 ,
,
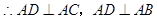 ,
,
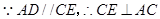
∴四邊形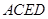 為直角梯形. (1分)
為直角梯形. (1分)
又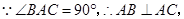
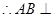 面
面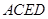 . (2分)
. (2分)
∴凸多面體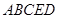 的體積
的體積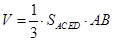
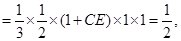
求得 .
(3分)
.
(3分)
取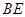 的中點G,連結
的中點G,連結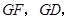 如圖:
如圖:
則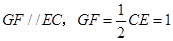 ,
,
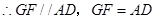 ,四邊形
,四邊形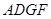 為平行四邊形,
為平行四邊形,
 .
(5分)
.
(5分)
又∵GD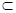 面BDE,AF
面BDE,AF 面BDE,
面BDE,
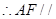 平面
平面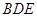 .
(7分)
.
(7分)
(Ⅱ)證明: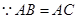 ,F為BC的中點,
,F為BC的中點,
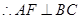 .
(8分)
.
(8分)
由(Ⅰ)知 平面
平面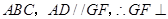 面
面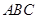 .
.
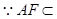 面
面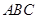 ,
,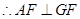 .
(9分)
.
(9分)
又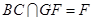 ,∴
,∴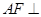 面
面 .
(10分)
.
(10分)
又∵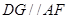 ,∴
,∴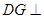 面
面 .
(11分)
.
(11分)
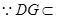 面
面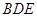 ,∴面
,∴面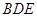 ⊥面
⊥面 . (12分)
. (12分)
考點:1.線面平行;2.線面垂直;3.面面垂直.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2011屆黑龍江省大慶實驗中學高三高考仿真模擬試題文數 題型:解答題
(本小題共12分)如圖所示, 平面
平面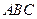 ,
, 平面
平面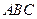 ,
,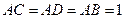 ,
,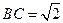 ,
,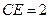 ,
,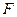 為
為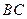 的中點.
的中點.
(Ⅰ)求證: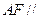 平面
平面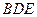 ;
;
(Ⅱ)求證:平面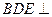 平面
平面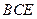 .
.
(Ⅲ)求凸多面體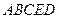 的體積為
的體積為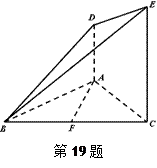
查看答案和解析>>
科目:高中數學 來源:2013屆廣東惠陽一中實驗學校高二6月月考文科數學試卷(解析版) 題型:解答題
(本小題滿分13分)如圖,正方形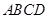 所在平面與三角形
所在平面與三角形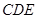 所在平面相交于
所在平面相交于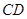 ,
,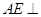 平面
平面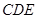 ,且
,且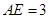 ,
,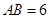

(1)求證: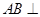 平面
平面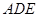 ;
;
(2)求凸多面體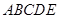 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com