
【題目】若圓錐的內切球(球面與圓錐的側面以及底面都相切)的半徑為1,當該圓錐體積取最小值時,該圓錐體積與其內切球體積比為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
解法一:設圓錐底面半徑為![]() ,高為
,高為![]() ,根據
,根據![]() ∽
∽![]() 可得
可得![]() ,即
,即![]() ,利用錐體的體積公式
,利用錐體的體積公式![]() ,然后利用基本不等式求最值;解法二:同解法一,利用導數求最值;解法三:設
,然后利用基本不等式求最值;解法二:同解法一,利用導數求最值;解法三:設![]() ,可得
,可得![]() ,
,![]() ,即
,即![]() ,設
,設![]() ,利用二次函數配方即可求解.
,利用二次函數配方即可求解.
解法一:如圖,設圓錐底面半徑為![]() ,高為
,高為![]() .
.
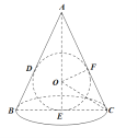
由![]() ∽
∽![]() 可得
可得![]() ,即
,即![]() ,
,
則![]() ,
,
所以![]() ,
,
因為![]() ,所以
,所以![]() ,當且僅當
,當且僅當![]() ,即
,即![]() 時取等號,
時取等號,
此時圓錐體積最小,最小值為![]() .因為該球的體積為
.因為該球的體積為![]() ,
,
所以該圓錐體積與其內切球體積比為![]() .
.
解法二: 如圖,設圓錐底面半徑為![]() ,高為
,高為![]() .
.

由![]() ∽
∽![]() 可得
可得![]() ,即
,即![]() ,
,
則![]() ,
,
所以![]() 令
令![]() ,
,
則![]() ,
,
當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ;
;
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,所以
上單調遞增,所以![]() ,
,
即![]() 時,該圓錐體積最小, 最小值為
時,該圓錐體積最小, 最小值為![]() .又其內切球體積為
.又其內切球體積為![]() .
.
所以該圓錐體積與其內切球體積比為![]() ,
,
解法三:設![]() ,則
,則![]() ,所以
,所以![]() ,
,
又![]()
![]() ,所以
,所以![]() ,
,
所以![]() ,令
,令![]() ,
,
因為![]() ,當且僅當
,當且僅當![]() 時取得最大值
時取得最大值![]() ,
,
從而圓錐體積最小,最小值為![]() .因為該球的體積為
.因為該球的體積為![]() ,
,
所以該圓錐體積與其內切球體積比為![]() ,
,
故選:D.


科目:高中數學 來源: 題型:
【題目】2019年以來,世界經濟和貿易增長放緩,中美經貿摩擦影響持續顯現,我國對外貿易仍然表現出很強的韌性.今年以來,商務部會同各省市全面貫徹落實穩外貿決策部署,出臺了一系列政策舉措,全力營造法治化國際化便利化的營商環境,不斷提高貿易便利化水平,外貿穩規模提質量轉動力取得階段性成效,進出口保持穩中提質的發展勢頭,如圖是某省近五年進出口情況統計圖,下列描述錯誤的是( )
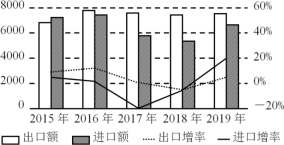
A.這五年,2015年出口額最少B.這五年,出口總額比進口總額多
C.這五年,出口增速前四年逐年下降D.這五年,2019年進口增速最快
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學中有許多形狀優美、寓意美好的曲線,如下圖就是在平面直角坐標系的“心形曲線”,又名RC心形線.如果以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,其RC心形線的極坐標方程為
軸正半軸為極軸,建立極坐標系,其RC心形線的極坐標方程為![]() .
.
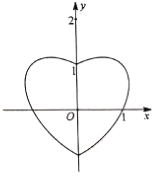
(1)求RC心形線的直角坐標方程;
(2)已知![]() 與直線
與直線![]() (
(![]() 為參數),若直線
為參數),若直線![]() 與RC心形線交于兩點
與RC心形線交于兩點![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了預防新型冠狀病毒的傳染,人員之間需要保持一米以上的安全距離.某公司會議室共有四行四列座椅,并且相鄰兩個座椅之間的距離超過一米,為了保證更加安全,公司規定在此會議室開會時,每一行、每一列均不能有連續三人就座.例如下圖中第一列所示情況不滿足條件(其中“√”表示就座人員).根據該公司要求,該會議室最多可容納的就座人數為( )
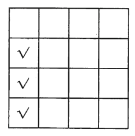
A.9B.10C.11D.12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(13分)
在平面直角坐標系xOy中,拋物線![]() 上異于坐標原點O的兩不同動點A、B滿足
上異于坐標原點O的兩不同動點A、B滿足![]() (如圖所示).
(如圖所示).
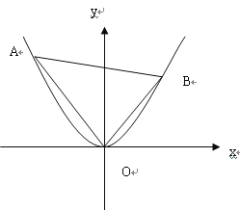
(Ⅰ)求![]() 得重心G(即三角形三條中線的交點)的軌跡方程;
得重心G(即三角形三條中線的交點)的軌跡方程;
(Ⅱ)![]() 的面積是否存在最小值?若存在,請求出最小值;若不存在,請說明理由.
的面積是否存在最小值?若存在,請求出最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一塊邊長為4的正方形鋁板(如圖),請設計一種裁剪方法,用虛線標示在答題卡本題圖中,通過該方案裁剪,可焊接做成一個密封的正四棱柱(底面是正方形且側棱垂于底面的四棱柱),且該四棱柱的全面積等于正方形鋁板的面積(要求裁剪的塊數盡可能少,不計焊接縫的面積),則該四棱柱外接球的體積為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為:
的參數方程為: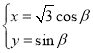 ,(
,(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的非負半軸為極軸建立極坐標系,直線l的極坐標方程為
軸的非負半軸為極軸建立極坐標系,直線l的極坐標方程為![]()
(1)求曲線![]() 和直線l的直角坐標方程;
和直線l的直角坐標方程;
(2)若點![]() 在曲線
在曲線![]() 上,且點
上,且點![]() 到直線l的距離最小,求點
到直線l的距離最小,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com