
【題目】已知p:|1﹣ ![]() |≤2,q:x2﹣2x+1﹣m2≤0(m>0).若“非p”是“非q”的必要而不充分條件,求實數m的取值范圍.
|≤2,q:x2﹣2x+1﹣m2≤0(m>0).若“非p”是“非q”的必要而不充分條件,求實數m的取值范圍.
【答案】解:解法一:由p:|1﹣ ![]() |≤2,解得﹣2≤x≤10, ∴“非p”:A={x|x>10或x<﹣2}、(3分)
|≤2,解得﹣2≤x≤10, ∴“非p”:A={x|x>10或x<﹣2}、(3分)
由q:x2﹣2x+1﹣m2≤0,解得1﹣m≤x≤1+m(m>0)
∴“非q”:B={x|x>1+m或x<1﹣m,m>0=(6分)
由“非p”是“非q”的必要而不充分條件可知:BA. 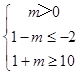 解得m≥9.
解得m≥9.
∴滿足條件的m的取值范圍為{m|m≥9}.(12分)
解法二:由“非p”是“非q”的必要而不充分條件.即“非q”“非p”,但“非p” ![]() “非q”,可以等價轉換為它的逆否命題:“pq,但q
“非q”,可以等價轉換為它的逆否命題:“pq,但q ![]() p”.即p是q的充分而不必要條件.
p”.即p是q的充分而不必要條件.
由|1﹣ ![]() |≤2,解得﹣2≤x≤10,
|≤2,解得﹣2≤x≤10,
∴p={x|﹣2≤x≤10}
由x2﹣2x+1﹣m2≤0,解得1﹣m≤x≤1+m(m>0)
∴q={x|1﹣m≤x≤1+m,m>0}
由p是q的充分而不必要條件可知:
pq 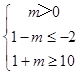 解得m≥9.
解得m≥9.
∴滿足條件的m的取值范圍為{m|m≥9}
【解析】思路一:“按題索驥”﹣﹣解不等式,求否命題,再根據充要條件的集合表示進行求解;思路二:本題也可以根據四種命題間的關系進行等價轉換,然后再根據充要條件的集合表示進行求解.
【考點精析】本題主要考查了解一元二次不等式和絕對值不等式的解法的相關知識點,需要掌握求一元二次不等式![]()
![]() 解集的步驟:一化:化二次項前的系數為正數;二判:判斷對應方程的根;三求:求對應方程的根;四畫:畫出對應函數的圖象;五解集:根據圖象寫出不等式的解集;規律:當二次項系數為正時,小于取中間,大于取兩邊;含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號才能正確解答此題.
解集的步驟:一化:化二次項前的系數為正數;二判:判斷對應方程的根;三求:求對應方程的根;四畫:畫出對應函數的圖象;五解集:根據圖象寫出不等式的解集;規律:當二次項系數為正時,小于取中間,大于取兩邊;含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】對定義域分別為D1 , D2的函數y=f(x),y=g(x),規定:函數h(x)= 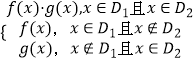 ,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),則h(x)的單調減區間是 .
,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),則h(x)的單調減區間是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,拋物線y=1﹣x2與x軸所圍成的區域是一塊等待開墾的土地,現計劃在該區域內圍出一塊矩形地塊ABCD作為工業用地,其中A、B在拋物線上,C、D在x軸上.已知工業用地每單位面積價值為3a元(a>0),其它的三個邊角地塊每單位面積價值a元.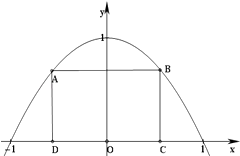
(1)求等待開墾土地的面積;
(2)如何確定點C的位置,才能使得整塊土地總價值最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的函數f(x)滿足 ![]() ,
, ![]() .
.
(1)求函數f(x)的解析式;
(2)求函數g(x)的單調區間;
(3)如果s、t、r滿足|s﹣r|≤|t﹣r|,那么稱s比t更靠近r.當a≥2且x≥1時,試比較 ![]() 和ex﹣1+a哪個更靠近lnx,并說明理由.
和ex﹣1+a哪個更靠近lnx,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com