已知函數f(x),當x、y∈R時,恒有f(x)-f(y)=f(x-y).
(Ⅰ)求證:f(x)是奇函數;
(Ⅱ)如果x<0時,f(x)>0,并且f(2)=-1,試求f(x)在區間[-2,6]上的最值;
(Ⅲ)在(Ⅱ)的條件下,對任意x∈[-2,6],不等式f(x)>m2+am-5對任意a∈[-1,1]恒成立,求實數m的取值范圍.
解:(Ⅰ)證明:∵當x、y∈R時,恒有f (x)-f (y)=f (x-y),
∴f (0)-f (0)=f (0-0),即f (0)=0,
∴f (0)-f (x)=f (0-x),
即-f (x)=f (-x),
所以f (x)是奇函數;
(Ⅱ)設x
1,x
2∈R且x
1<x
2,
則f(x
1)-f(x
2)=f(x
1-x
2),
∵x
1<x
2,∴x
1-x
2<0,
∴f(x
1-x
2)>0,即f(x
1>f(x
2),
故,函數f(x)在R上單調遞減,
所以,函數f(x)在[-2,6]上單調遞減,
故,f(x)
max=f(-2)=-f(2)=1,
f(x)
min=f(6)=f(4)+f(2)=3f(2)=-3;
(Ⅲ)∵對任意x∈[-2,6],不等式f(x)>m
2+am-5恒成立,
∴m
2+am-5<f(x)
min=-3,即m
2+am-2<0,
∵對任意a∈[-1,1],不等式m
2+am-2<0恒成立,
∴
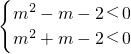
,解得-1<m<1,
所以,實數m的取值范圍是:-1<m<1.
分析:(Ⅰ)定義法:令x=y=0,可求出f(0),再令x=0,y=x,即可證明;
(Ⅱ)先利用定義判斷f(x)的單調性,再利用單調性及f(2)=-1即可求出f(x)在區間[-2,6]上的最值;
(Ⅲ)對任意x∈[-2,6],不等式f(x)>m
2+am-5恒成立,等價于m
2+am-5<f(x)
min,又對任意a∈[-1,1]恒成立,可得
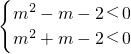
,由此可求出m的范圍;
點評:本題考查抽象函數的奇偶性、單調性及函數恒成立問題,考查學生分析問題解決問題的能力,對函數恒成立問題常轉化為函數最值問題解決,體現了轉化思想.

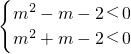 ,解得-1<m<1,
,解得-1<m<1,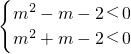 ,由此可求出m的范圍;
,由此可求出m的范圍;

 名校課堂系列答案
名校課堂系列答案