

 經(jīng)過點
經(jīng)過點 ,一個焦點是
,一個焦點是 .
. 的方程;
的方程; 與
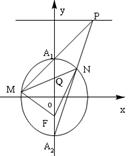
與 軸的兩個交點為
軸的兩個交點為 、
、 ,點
,點 在直線
在直線 上,直線
上,直線 、
、 分別與橢圓
分別與橢圓 交于
交于 、
、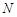 兩點.試問:當點
兩點.試問:當點 在直線
在直線 上運動時,直線
上運動時,直線 是否恒經(jīng)過定點
是否恒經(jīng)過定點 ?證明你的結(jié)論.
?證明你的結(jié)論.
 在直線
在直線 上運動時,直線
上運動時,直線 恒經(jīng)過定點
恒經(jīng)過定點 .
. ,再根據(jù)橢圓過點
,再根據(jù)橢圓過點 ,由橢圓的定義可求出
,由橢圓的定義可求出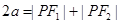 ,利用
,利用 ,求出b,焦點在y軸上,所以橢圓方程確定.
,求出b,焦點在y軸上,所以橢圓方程確定. 在
在 軸上時,
軸上時, 、
、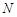 分別與
分別與 、
、 重合,
重合, 通過定點
通過定點 ,則
,則 必在
必在 軸上,設
軸上,設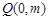 ,當點
,當點 不在
不在 軸上時,設
軸上時,設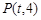 ,
,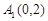 、
、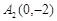 ,
,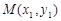 ,
,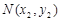 ,然后分別表示出PA1和PA2的方程,分別與橢圓C方程聯(lián)立求出M,N的坐標,進而得到向量
,然后分別表示出PA1和PA2的方程,分別與橢圓C方程聯(lián)立求出M,N的坐標,進而得到向量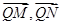 的坐標,再根據(jù)
的坐標,再根據(jù)
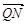 ,得到
,得到 ,因而求出m=1,從而得到定點Q(1,0).
,因而求出m=1,從而得到定點Q(1,0).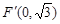 ,
,
 在
在 軸上時,
軸上時, 、
、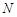 分別與
分別與 、
、 重合,
重合, 通過定點
通過定點 ,則
,則 必在
必在 軸上,設
軸上,設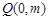 ,………………(6分)
,………………(6分) 不在
不在 軸上時,設
軸上時,設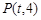 ,
,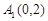 、
、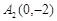 ,
,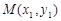 ,
,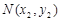
 方程
方程 ,
, 方程
方程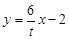 ,
, 代入
代入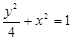 得
得 ,
,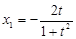 ,
,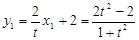 ,
,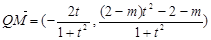 , ……………(9分)
, ……………(9分)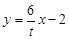 代入
代入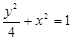 得
得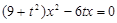
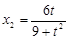 ,
, ,
, 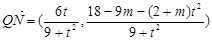 , ………………(11分)
, ………………(11分)
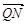 ,
,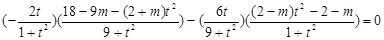 ,
, ,
,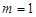 ,
, 在直線
在直線 上運動時,直線
上運動時,直線 恒經(jīng)過定點
恒經(jīng)過定點 .……(15分)
.……(15分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
 PD.
PD.
 的直線被C所截線段的長度.
的直線被C所截線段的長度.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
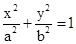 (a>b>0)的離心率為
(a>b>0)的離心率為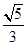 ,短軸一個端點到右焦點的距離為3.
,短軸一個端點到右焦點的距離為3.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
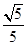 的橢圓
的橢圓 :
: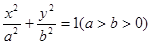 的左、右焦點分別為
的左、右焦點分別為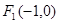 、
、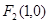 ,
,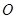 是坐標原點.
是坐標原點. 的方程;
的方程; 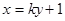 與
與 交于相異兩點
交于相異兩點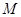 、
、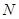 ,且
,且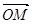

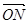
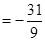 ,求
,求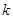 .(其中
.(其中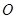 是坐標原點)
是坐標原點)查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com