
【題目】設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,上頂點為
,上頂點為![]() ,過點
,過點![]() 與
與![]() 垂直的直線交
垂直的直線交![]() 軸負半軸于點
軸負半軸于點![]() ,且
,且![]() ,過
,過![]() ,
,![]() 三點的圓恰好與直線
三點的圓恰好與直線![]() 相切.
相切.
![]() 求橢圓
求橢圓![]() 的方程;
的方程;
![]() 過右焦點
過右焦點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,問在
兩點,問在![]() 軸上是否存在點
軸上是否存在點![]() ,使得以
,使得以![]() 為鄰邊的平行四邊形是菱形?如果存在,求出
為鄰邊的平行四邊形是菱形?如果存在,求出![]() 的取值范圍;如果不存在,說明理由.
的取值范圍;如果不存在,說明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
![]() 設點
設點![]() 的坐標為
的坐標為![]() ,且
,且![]() ,利用
,利用![]() 以及
以及![]() 得出點
得出點![]() 的坐標,利用外接圓圓心
的坐標,利用外接圓圓心![]() 到該直線的距離等于半徑,可求出
到該直線的距離等于半徑,可求出![]() 的值,進而得出
的值,進而得出![]() 與
與![]() 的值,從而得出橢圓
的值,從而得出橢圓![]() 的方程;
的方程;![]() 令
令![]() ,得出
,得出![]() ,設點
,設點![]() 、
、![]() ,將直線l的方程與橢圓
,將直線l的方程與橢圓![]() 的方程聯立,利用韋達定理,求出線段
的方程聯立,利用韋達定理,求出線段![]() 的中點
的中點![]() 的坐標,將條件“以
的坐標,將條件“以![]() 為鄰邊的平行四邊形是菱形”轉化為
為鄰邊的平行四邊形是菱形”轉化為![]() ,得出這兩條直線的斜率之積為
,得出這兩條直線的斜率之積為![]() ,然后得出
,然后得出![]() 的表達式,利用不等式的性質可求出實數
的表達式,利用不等式的性質可求出實數![]() 的取值范圍.
的取值范圍.
![]() 設橢圓C的焦距為
設橢圓C的焦距為![]() ,則點
,則點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,設點Q的坐標為
,設點Q的坐標為![]() ,且
,且![]() ,
,
如下圖所示,
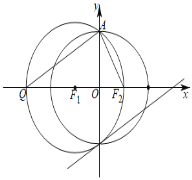
![]() ,
,![]() ,
,
![]() ,則
,則![]() ,所以,
,所以,![]() ,則點Q的坐標為
,則點Q的坐標為![]() ,
,
![]() 直線
直線![]() 與直線AQ垂直,且點
與直線AQ垂直,且點![]() ,所以,
,所以,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,則
,則![]() ,
,![]() .
.
![]() 為直角三角形,且
為直角三角形,且![]() 為斜邊,
為斜邊,
線段![]() 的中點為
的中點為![]() ,
,![]() 的外接圓半徑為2c.
的外接圓半徑為2c.
由題意可知,點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
所以,![]() ,
,![]() ,
,![]() ,
,
因此,橢圓C的方程為![]() .
.
![]() 由題意知,直線
由題意知,直線![]() 的斜率
的斜率![]() ,并設
,并設![]() ,則直線l的方程為
,則直線l的方程為![]() ,
,
設點![]() 、
、![]()
將直線![]() 的方程與橢圓C的方程聯立
的方程與橢圓C的方程聯立 ,
,
消去x得![]() ,
,
由韋達定理得![]() ,
,![]() .
.
![]() ,
,![]() .
.
所以,線段MN的中點為點![]() .
.
由于以PM,PN為鄰邊的平行四邊形是菱形,則![]() ,則
,則![]() ,所以,
,所以,![]() .
.
由兩點連線的斜率公式可得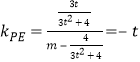 ,得
,得![]() .
.
由于![]() ,則
,則![]() ,所以,
,所以,![]() ,所以,
,所以,![]() .
.
因此,在x軸上存在點![]() ,使得以PM,PN為鄰邊的平行四邊形是菱形,
,使得以PM,PN為鄰邊的平行四邊形是菱形,
且實數m的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】某人事部門對參加某次專業技術考試的100人的成績進行了統計,繪制的頻率分布直方圖如圖所示.規定80分以上者晉級成功,否則晉級失敗(滿分為100分).
(1)求圖中![]() 的值;
的值;
(2)估計該次考試的平均分![]() (同一組中的數據用該組的區間中點值代表);
(同一組中的數據用該組的區間中點值代表);
(3)根據已知條件完成下面2×2列聯表,并判斷能否有85%的把握認為“晉級成功”與性別有關.
晉級成功 | 晉級失敗 | 合計 | |
男 | 16 | ||
女 | 50 | ||
合計 |

參考公式:![]() ,其中
,其中![]()
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人設計一項單人游戲,規則如下:先將一棋子放在如圖所示正方形![]() (邊長為2個單位)的頂點
(邊長為2個單位)的頂點![]() 處,然后通過擲骰子來確定棋子沿正方形的邊按逆時針方向行走的單位,如果擲出的點數為
處,然后通過擲骰子來確定棋子沿正方形的邊按逆時針方向行走的單位,如果擲出的點數為![]() ,則棋子就按逆時針方向行走
,則棋子就按逆時針方向行走![]() 個單位,一直循環下去.則某人拋擲三次骰子后棋子恰好又回到點
個單位,一直循環下去.則某人拋擲三次骰子后棋子恰好又回到點![]() 處的所有不同走法共有( )
處的所有不同走法共有( )

A. 22種 B. 24種 C. 25種 D. 27種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】男運動員6名,女運動員4名,其中男女隊長各1名.選派5人外出比賽,在下列情形中各有多少種選派方法?
(1)男運動員3名,女運動員2名;
(2)至少有1名女運動員;
(3)隊長中至少有1人參加;
(4)既要有隊長,又要有女運動員.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定下列四個命題
![]() 若一個平面內的兩條直線與另一個平面都平行,那么這兩個平面相互平行;
若一個平面內的兩條直線與另一個平面都平行,那么這兩個平面相互平行;
![]() 若一條直線和兩個互相垂直的平面中的一個平面垂直,那么這條直線一定平行于另一個平面;
若一條直線和兩個互相垂直的平面中的一個平面垂直,那么這條直線一定平行于另一個平面;
![]() 若一條直線和兩個平行平面中的一個平面垂直,那么這條直線也和一個平面垂直;
若一條直線和兩個平行平面中的一個平面垂直,那么這條直線也和一個平面垂直;
![]() 若兩個平面垂直,那么一個平面內與它們的交線不垂直的直線與另一個平面也不垂直,
若兩個平面垂直,那么一個平面內與它們的交線不垂直的直線與另一個平面也不垂直,
其中,真命題的個數是![]()
![]()
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求實數a的取值范圍.
(a>0)恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com