
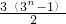
 ,進而對1或-1、
,進而對1或-1、 或-
或- 分別分析可得其可能的情況數(shù)目,由分步計數(shù)原理計算可得答案;當集合An={1,2,…,n}是解析式為y=x2的函數(shù)的值域時,其定義域中可能有的元素有±1、±
分別分析可得其可能的情況數(shù)目,由分步計數(shù)原理計算可得答案;當集合An={1,2,…,n}是解析式為y=x2的函數(shù)的值域時,其定義域中可能有的元素有±1、± 、±
、± 、±2、…±
、±2、…± ,且每對相反數(shù)至少有一個,進而對每對相反數(shù)依次分析可得其可能的情況數(shù)目,由分步計數(shù)原理計算可得an的值,即可得{an}為等比數(shù)列,再用等比數(shù)列前n和公式求出a1+a2+…+an的值.
,且每對相反數(shù)至少有一個,進而對每對相反數(shù)依次分析可得其可能的情況數(shù)目,由分步計數(shù)原理計算可得an的值,即可得{an}為等比數(shù)列,再用等比數(shù)列前n和公式求出a1+a2+…+an的值. ,且每對相反數(shù)至少有一個,
,且每對相反數(shù)至少有一個, 或-
或- ,兩個中任取一個或全部都取,有3種情況;
,兩個中任取一個或全部都取,有3種情況; 、±
、± 、±2、…±
、±2、…± ,且每組至少有一個,
,且每組至少有一個, 或-
或- ,兩個中任取一個或全部都取,有3種情況;
,兩個中任取一個或全部都取,有3種情況; 或-
或- ,兩個中任取一個或全部都取,有3種情況;
,兩個中任取一個或全部都取,有3種情況;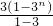 =
=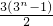 ;
;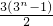 .
.

 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數(shù)學 來源: 題型:
| 3(3n-1) |
| 2 |
| 3(3n-1) |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
已知函數(shù)f(x)=ax3-x2+cx(a≠0)的圖像如下所示,它與x軸僅有兩個交點O(0,0)和A(xA,0)(xA>0).
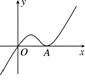
(1)證明:常數(shù)c≠0;
(2)如果xA=![]() ,求函數(shù)f(
,求函數(shù)f(![]() x)的解析式.
x)的解析式.
查看答案和解析>>
科目:高中數(shù)學 來源:2009-2010學年北京大學附中高三(上)入學摸底數(shù)學試卷(理科)(解析版) 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com