
(本小題滿分l2分)(注意:在試題卷上作答無效)
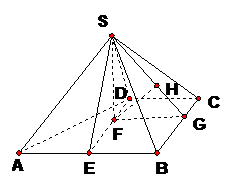
如圖,四棱錐 中,
中, 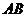 ∥
∥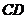 ,
, ,側面
,側面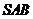 為等邊三角形.
為等邊三角形.  .
.
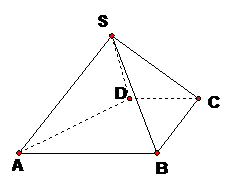
(I) 證明:
(II) 求AB與平面SBC所成角的大小。
【思路點撥】第(I)問的證明的突破口是利用等邊三角形SAB這個條件,找出AB的中點E,連結SE,DE,就做出了解決這個問題的關鍵輔助線。
(II)本題直接找線面角不易找出,要找到與AB平行的其它線進行轉移求解。
【精講精析】證明:(I)取AB中點E,連結DE,則四邊形BCDE為矩形,DE=CB=2。
 連結SE,則
連結SE,則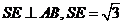
又SD=1,故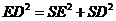
所以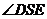 為直角。
為直角。
由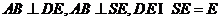 ,得
,得
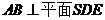 ,所以
,所以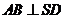 .
.
SD與兩條相交直線AB、SE都垂直。
所以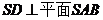
(II)由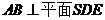 知,
知,
作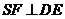 ,垂足為F,則
,垂足為F,則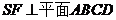 ,
,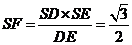
作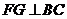 ,垂足為G,則FG=DC=1。
,垂足為G,則FG=DC=1。
連結SG,則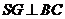
又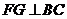 ,
,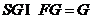 ,故
,故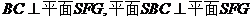 ,
,
作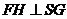 ,H為垂足,則
,H為垂足,則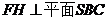 .
.
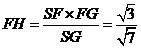
即F到平面SBC的距離為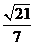 。
。
由于ED//BC,所以ED//平面SBC,E到平面SBC的距離d也為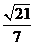 。
。
設AB與平面SBC所成的角為 ,則
,則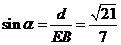 ,
,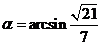 .
.
解法二:
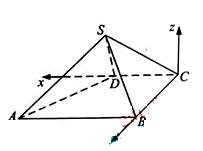 以C為坐標原點,射線CD為x軸正半軸,建立如圖所示的直角坐標系C-xyz,設D(1,0,0),則A(2,2,0),B(0,2,0)。
以C為坐標原點,射線CD為x軸正半軸,建立如圖所示的直角坐標系C-xyz,設D(1,0,0),則A(2,2,0),B(0,2,0)。
又設S(x,y,z),則x>0,y>0,z>0.
(I)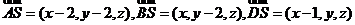
由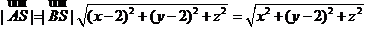 得
得
故x=1.
由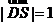 得
得 ,
,
又由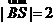 得,
得,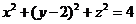
即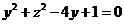 ,故
,故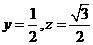 。
。
于是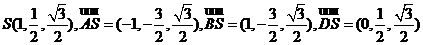 ,
,
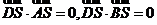
故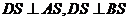 ,又
,又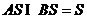
所以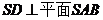 .
.
(II)設平面SBC的法向量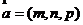 ,
,
則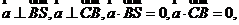
又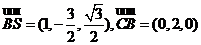
故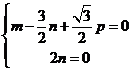
取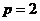 得
得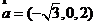 ,又
,又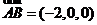
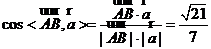 .
.
故AB與平面SBC所成的角為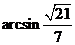 .
.


科目:高中數學 來源:2011-2012學年山東省高三下學期模擬沖刺考試理科數學試卷(解析版) 題型:解答題
(本小題滿分l2分)已知數列{an}中,a1=1,a2=3且2an+1=an+2+an(n∈N*).數列{bn}的前n項和為Sn,其中b1=- ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*).
(1)求數列{an}和{bn}的通項公式;
(2)若Tn= +
+ +…+
+…+ ,求Tn的表達式
,求Tn的表達式
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三下學期模擬沖刺考試理科數學試卷(解析版) 題型:解答題
(本小題滿分l2分)已知橢圓的的右頂點為A,離心率 ,過左焦點
,過左焦點 作直線
作直線 與橢圓交于點P,Q,直線AP,AQ分別與直線
與橢圓交于點P,Q,直線AP,AQ分別與直線 交于點
交于點 .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)證明以線段 為直徑的圓經過焦點
為直徑的圓經過焦點 .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年貴州省高三年級第五次月考文科數學 題型:解答題
(本小題滿分l2分)(注意:在試題卷上作答無效)
求經過A(2,-1),和直線x+y=1相切,且圓心在直線y=-2x上的圓的方程
(I)求出圓的標準方程
(II)求出(I)中的圓與直線3x+4y=0相交的弦長AB
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省高三上學期10月月考理科數學卷 題型:解答題
(本小題滿分l2分)設命題 :函數
:函數 (
( )的值域是
)的值域是 ;命題
;命題 :指數函數
:指數函數 在
在 上是減函數.若命題“
上是減函數.若命題“ 或
或 ”是假命題,求實數
”是假命題,求實數 的范圍.
的范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com