
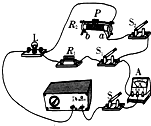
 如圖所示電路中,燈泡L標有“3V”且燈絲電阻不變.電源兩端電壓為U保持不變,R1為定值電阻,R2為滑動變阻器.當只閉合開關S、S1時,燈泡的功率是額定功率的四分之一.當只閉合開關S、S2時,調節滑動變阻器的滑片P,使其位于a點時(圖中表示a點的大致位置),燈泡正常發光,電流表的示數是0.3A,滑動變阻器的功率為Pa;保持開關狀態不變,滑動變阻器的滑片P移至b端時,滑動變阻器接入電路的電阻最大,此時燈泡的功率是額定功率的九分之一,滑動變阻器的功率為Pb,且知Pa:Pb=9:5.
如圖所示電路中,燈泡L標有“3V”且燈絲電阻不變.電源兩端電壓為U保持不變,R1為定值電阻,R2為滑動變阻器.當只閉合開關S、S1時,燈泡的功率是額定功率的四分之一.當只閉合開關S、S2時,調節滑動變阻器的滑片P,使其位于a點時(圖中表示a點的大致位置),燈泡正常發光,電流表的示數是0.3A,滑動變阻器的功率為Pa;保持開關狀態不變,滑動變阻器的滑片P移至b端時,滑動變阻器接入電路的電阻最大,此時燈泡的功率是額定功率的九分之一,滑動變阻器的功率為Pb,且知Pa:Pb=9:5.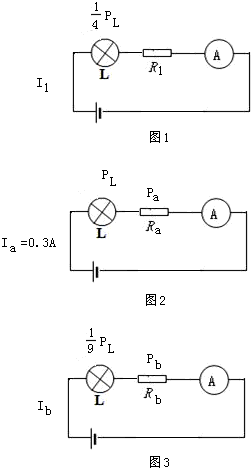 解:當只閉合開關S、S1時,等效電路圖如圖1所示;
解:當只閉合開關S、S1時,等效電路圖如圖1所示;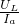 =
=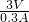 =10Ω.
=10Ω. PL=Ib2RL,
PL=Ib2RL, Ia=
Ia= ×0.3A=0.1A,
×0.3A=0.1A,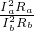 =
= ,
, PL=I12RL,
PL=I12RL, Ia=
Ia= ×0.3A=0.15A,
×0.3A=0.15A,

科目:初中物理 來源: 題型:
 (2011?宜賓縣一模)如圖所示電路中,燈泡L1上標有“8V,4W”,L2上標有“12V,9W”,閉合開關后,為了安全,使其中一盞燈剛好正常發光不燒壞,電源電壓最大為
(2011?宜賓縣一模)如圖所示電路中,燈泡L1上標有“8V,4W”,L2上標有“12V,9W”,閉合開關后,為了安全,使其中一盞燈剛好正常發光不燒壞,電源電壓最大為查看答案和解析>>
科目:初中物理 來源: 題型:
 如圖所示電路中,燈泡L1上標有“24V,8W”,L2上標有“24V,16W”,開關閉合后燈泡L1正常工作,電流表A1的示數是
如圖所示電路中,燈泡L1上標有“24V,8W”,L2上標有“24V,16W”,開關閉合后燈泡L1正常工作,電流表A1的示數是查看答案和解析>>
科目:初中物理 來源: 題型:
 如圖所示電路中,燈泡L上標有“6V 9W”字樣,閉合開關S后,燈泡正常發光,電壓表V1的示數為U1,電壓表V2的示數為U2,若U1:U2=2:3,下列說法錯誤的是( )
如圖所示電路中,燈泡L上標有“6V 9W”字樣,閉合開關S后,燈泡正常發光,電壓表V1的示數為U1,電壓表V2的示數為U2,若U1:U2=2:3,下列說法錯誤的是( )查看答案和解析>>
科目:初中物理 來源: 題型:
 (2010?朝陽區一模)如圖所示電路中,燈泡L標有“3V”且燈絲電阻不變.電源兩端電壓為U保持不變,R1為定值電阻,R2為滑動變阻器.當只閉合開關S、S1時,燈泡的功率是額定功率的四分之一.當只閉合開關S、S2時,調節滑動變阻器的滑片P,使其位于a點時(圖中表示a點的大致位置),燈泡正常發光,電流表的示數是0.3A,滑動變阻器的功率為Pa;保持開關狀態不變,滑動變阻器的滑片P移至b端時,滑動變阻器接入電路的電阻最大,此時燈泡的功率是額定功率的九分之一,滑動變阻器的功率為Pb,且知Pa:Pb=9:5.
(2010?朝陽區一模)如圖所示電路中,燈泡L標有“3V”且燈絲電阻不變.電源兩端電壓為U保持不變,R1為定值電阻,R2為滑動變阻器.當只閉合開關S、S1時,燈泡的功率是額定功率的四分之一.當只閉合開關S、S2時,調節滑動變阻器的滑片P,使其位于a點時(圖中表示a點的大致位置),燈泡正常發光,電流表的示數是0.3A,滑動變阻器的功率為Pa;保持開關狀態不變,滑動變阻器的滑片P移至b端時,滑動變阻器接入電路的電阻最大,此時燈泡的功率是額定功率的九分之一,滑動變阻器的功率為Pb,且知Pa:Pb=9:5.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com