
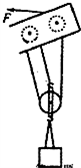
 如圖所示的是建筑工地上正在運行的一臺起重機吊臂上的滑輪組,由電動機向滑輪組提供動力,不計一切摩擦和繩重,已知動滑輪和吊鉤共重200N,在拉力F的作用下,把重2.98×104N的重物勻速提高20m,拉力做功的功率為1.5×104W,求:
如圖所示的是建筑工地上正在運行的一臺起重機吊臂上的滑輪組,由電動機向滑輪組提供動力,不計一切摩擦和繩重,已知動滑輪和吊鉤共重200N,在拉力F的作用下,把重2.98×104N的重物勻速提高20m,拉力做功的功率為1.5×104W,求: =
= ≈99.3%.
≈99.3%.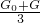 =
=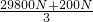 =10000N,
=10000N,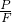 =
=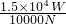 =1.5m/s.
=1.5m/s.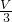 =
= =0.5m/s.
=0.5m/s. 求出效率.
求出效率.

 期末集結號系列答案
期末集結號系列答案科目:初中物理 來源: 題型:
 如圖所示,是建筑工地常用來搬運磚塊的兩種機械(滑輪組和起重機).觀察丙圖和
如圖所示,是建筑工地常用來搬運磚塊的兩種機械(滑輪組和起重機).觀察丙圖和查看答案和解析>>
科目:初中物理 來源: 題型:
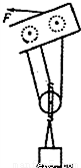
 如圖所示的是建筑工地上正在運行的一臺起重機吊臂上的滑輪組,由電動機向滑輪組提供動力,不計一切摩擦和繩重,已知動滑輪和吊鉤共重200N,在拉力F的作用下,把重2.98×104N的重物勻速提高20m,拉力做功的功率為1.5×104W,求:
如圖所示的是建筑工地上正在運行的一臺起重機吊臂上的滑輪組,由電動機向滑輪組提供動力,不計一切摩擦和繩重,已知動滑輪和吊鉤共重200N,在拉力F的作用下,把重2.98×104N的重物勻速提高20m,拉力做功的功率為1.5×104W,求:查看答案和解析>>
科目:初中物理 來源:2008年江蘇省蘇州市吳江市桃源中學中考物理二模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com