
 如圖所示電路,設電源電壓不變,燈絲電阻不隨溫度變化.當只閉合開關S1時,電流表的示數是I1.當只閉合開關S2時,電流表的示數是I2.當開關S1、S2都閉合時,燈L正常發光,電流表的示數為I3.當開關S1、S2都斷開時,電流表的示數是I4,電壓表V1、V2示數之比為3:1,此時RL消耗的電功率為0.5W;已知I1:I2=3:1,求:
如圖所示電路,設電源電壓不變,燈絲電阻不隨溫度變化.當只閉合開關S1時,電流表的示數是I1.當只閉合開關S2時,電流表的示數是I2.當開關S1、S2都閉合時,燈L正常發光,電流表的示數為I3.當開關S1、S2都斷開時,電流表的示數是I4,電壓表V1、V2示數之比為3:1,此時RL消耗的電功率為0.5W;已知I1:I2=3:1,求:
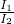 =
=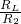 =
= ,
,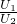 =
= =
= =
=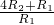 =
=
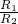 =
= ;
;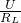 +
+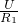 +
+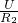 =
= +
+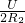 +
+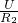 =
=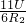 ,
,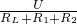 =
= =
=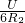 ,
,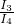 =
= =
= ;
;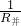 =
=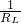 +
+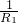 +
+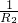 =
=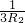 +
+ +
+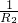 =
=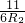 ,
, =
=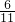 ×
×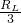 =
= ,
, =
= ×
×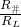 =(
=( )2×
)2×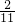 =
=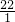 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中物理 來源: 題型:
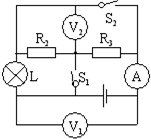 (2009?石景山區一模)如圖所示電路,設電源電壓不變,燈絲電阻不隨溫度變化.當只閉合開關S1時,電流表的示數是I1.當只閉合開關S2時,電流表的示數是I2.當斷開S1、S2時,電流表的示數是I3,電壓表V1、V2示數之比為2:1,此時RL消耗的電功率為0.24W;當開關S1、S2閉合時,燈L正常發光,電流表的示數為I4.已知I1:I2=2:1,(電路圖中所有的交叉點都相連)求:
(2009?石景山區一模)如圖所示電路,設電源電壓不變,燈絲電阻不隨溫度變化.當只閉合開關S1時,電流表的示數是I1.當只閉合開關S2時,電流表的示數是I2.當斷開S1、S2時,電流表的示數是I3,電壓表V1、V2示數之比為2:1,此時RL消耗的電功率為0.24W;當開關S1、S2閉合時,燈L正常發光,電流表的示數為I4.已知I1:I2=2:1,(電路圖中所有的交叉點都相連)求:查看答案和解析>>
科目:初中物理 來源: 題型:
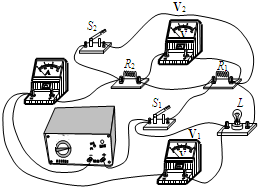 (2013?東城區一模)如圖所示電路,設電源電壓不變,燈絲電阻不隨溫度變化.當只閉合開關S1時,電流表的示數是I1.當只閉合開關S2時,電流表的示數是I2.當開關S1、S2都閉合時,燈L正常發光,電流表的示數為I3.當開關S1、S2都斷開時,電流表的示數是I4,電壓表V1、V2示數之比為3:1,此時RL消耗的電功率為0.5W;已知I1:I2=3:1,求:
(2013?東城區一模)如圖所示電路,設電源電壓不變,燈絲電阻不隨溫度變化.當只閉合開關S1時,電流表的示數是I1.當只閉合開關S2時,電流表的示數是I2.當開關S1、S2都閉合時,燈L正常發光,電流表的示數為I3.當開關S1、S2都斷開時,電流表的示數是I4,電壓表V1、V2示數之比為3:1,此時RL消耗的電功率為0.5W;已知I1:I2=3:1,求:查看答案和解析>>
科目:初中物理 來源: 題型:
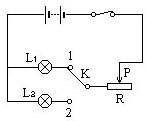 如圖所示電路,設電源電壓恒定,滑動變阻器的最大阻值為16歐,燈L1標有“6V 3W”,燈L2標有“6V 6W”,燈絲電阻不隨溫度變化.當開關K在接點1位置時,滑動變阻器滑片P位于中點,燈L1正常發光;當開關K由接點1轉到接點2時,適當調節滑片P的位置,使燈L2也能正常發光.
如圖所示電路,設電源電壓恒定,滑動變阻器的最大阻值為16歐,燈L1標有“6V 3W”,燈L2標有“6V 6W”,燈絲電阻不隨溫度變化.當開關K在接點1位置時,滑動變阻器滑片P位于中點,燈L1正常發光;當開關K由接點1轉到接點2時,適當調節滑片P的位置,使燈L2也能正常發光.查看答案和解析>>
科目:初中物理 來源: 題型:
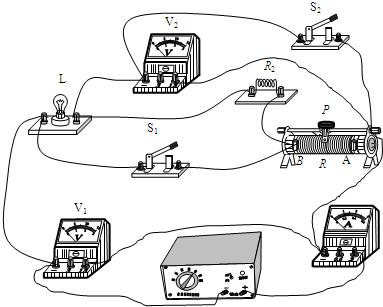 (2011?北京二模)如圖所示電路,設電源電壓不變,燈絲電阻不隨溫度變化,滑動變阻器的最大阻值為R.當開關S1、S2斷開,滑動變阻器的滑片P位于A端時,電壓表V2示數為U2,電阻R2和滑動變阻器消耗的總功率為P1=2.4W;當開關S1斷開,S2閉合時,電壓表V1示數為U1,燈正常發光,電流表的示數為I;當開關S1、S2都閉合時,接入電路的滑動變阻器阻值為最大值的2/3時,電流表的示數與I相比變化了△I=1.4A,滑動變阻器消耗的電功率為P2=14.7W.已知U1:U2=7:6.求:
(2011?北京二模)如圖所示電路,設電源電壓不變,燈絲電阻不隨溫度變化,滑動變阻器的最大阻值為R.當開關S1、S2斷開,滑動變阻器的滑片P位于A端時,電壓表V2示數為U2,電阻R2和滑動變阻器消耗的總功率為P1=2.4W;當開關S1斷開,S2閉合時,電壓表V1示數為U1,燈正常發光,電流表的示數為I;當開關S1、S2都閉合時,接入電路的滑動變阻器阻值為最大值的2/3時,電流表的示數與I相比變化了△I=1.4A,滑動變阻器消耗的電功率為P2=14.7W.已知U1:U2=7:6.求:查看答案和解析>>
科目:初中物理 來源: 題型:
 如圖所示電路,設電源電壓不變.當只閉合開關S1時,電流表的示數是I1;當只閉合開關S2時,電流表的示數是I2;已知I1:I2=2:1.當通過控制開關S1和S2,使電路消耗的最大功率和最小功率分別為P總和P總′,已知電路消耗的總功率達到最小時,電壓表V1、V2的示數之比為2:1,電阻R2消耗的電功率P2′為2W,求:
如圖所示電路,設電源電壓不變.當只閉合開關S1時,電流表的示數是I1;當只閉合開關S2時,電流表的示數是I2;已知I1:I2=2:1.當通過控制開關S1和S2,使電路消耗的最大功率和最小功率分別為P總和P總′,已知電路消耗的總功率達到最小時,電壓表V1、V2的示數之比為2:1,電阻R2消耗的電功率P2′為2W,求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com