
科目: 來源: 題型:
【題目】某地質量監管部門對轄區內的甲、乙兩家企業生產的某同類產品進行檢查,分別隨機抽取了50件產品并對某一項關鍵質量指標做檢測,獲得了它們的質量指標值s,并對樣本數據(質量指標值s)進行了整理、描述和分析.下面給出了部分信息.
a.該質量指標值對應的產品等級如下:
質量指標值 |
|
|
|
|
|
等級 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
說明:等級是一等品,二等品為質量合格(其中等級是一等品為質量優秀).
等級是次品為質量不合格.
b.甲企業樣本數據的頻數分布統計表如下(不完整).
c.乙企業樣本數據的頻數分布直方圖如下.
甲企業樣本數據的頻數分布表
分組 | 頻數 | 頻率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合計 | 50 | 1.00 |
乙企業樣本數據的頻數分布直方圖
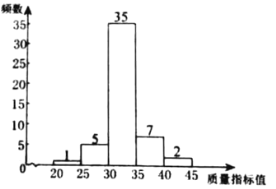
d.兩企業樣本數據的平均數、中位數、眾數、極差、方差如下:
平均數 | 中位數 | 眾數 | 極差 | 方差 | |
甲企業 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企業 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根據以上信息,回答下列問題:
(1)m的值為________,n的值為________.
(2)若從甲企業生產的產品中任取一件,估計該產品質量合格的概率為________;若乙企業生產的某批產品共5萬件,估計質量優秀的有________萬件;
(3)根據圖表數據,你認為________企業生產的產品質量較好,理由為______________.(從某個角度說明推斷的合理性)
查看答案和解析>>
科目: 來源: 題型:
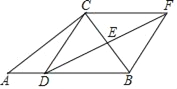
【題目】如圖,在△ABC中,D是AB邊上任意一點,E是BC邊中點,過點C作AB的平行線,交DE的延長線于點F,連接BF,CD.
(1)求證:四邊形CDBF是平行四邊形;
(2)若∠FDB=30°,∠ABC=45°,BC=4![]() ,求DF的長.
,求DF的長.
查看答案和解析>>
科目: 來源: 題型:
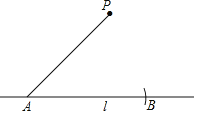
【題目】在數學課上,老師提出如下問題:如何使用尺規完成“過直線l外一點P作已知直線l的平行線”.
小明的作法如下:
①在直線l上取一點A,以點A為圓心,AP長為半徑作弧,交直線l于點B;
②分別以P,B為圓心,以AP長為半徑作弧,兩弧相交于點Q(與點A不重合);
③作直線PQ.所以直線PQ就是所求作的直線.根據小明的作圖過程,
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:∵AB=AP= = .
∴四邊形ABQP是菱形( )(填推理的依據).
∴PQ∥l.
查看答案和解析>>
科目: 來源: 題型:
【題目】2017年全球超級計算機500強名單公布,中國超級計算機“神威·太湖之光”和“天河二號”攜手奪得前兩名.已知“神威·太湖之光”的浮點運算速度是“天河二號”的2.74倍.這兩種超級計算機分別進行100億億次浮點運算,“神威·太湖之光”的運算時間比“天河二號”少18.75秒,求這兩種超級計算機的浮點運算速度.設“天河二號”的浮點運算速度為![]() 億億次/秒,依題意,可列方程為___________.
億億次/秒,依題意,可列方程為___________.
查看答案和解析>>
科目: 來源: 題型:
【題目】太陽能是來自太陽的輻射能量,對于地球上的人類來說,太陽能是對環境無任何污染的可再生能源,因此許多國家都在大陸發展太陽能.如圖是2013-2017年我國光伏發電裝機容量統計圖.根據統計圖提供的信息,判斷下列說法不合理的是( )
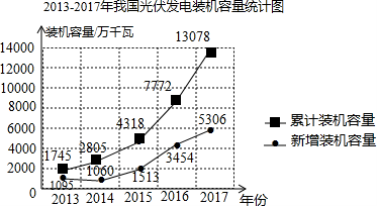
A.截至2017年底,我國光伏發電累計裝機容量為13078萬千瓦
B.2013-2017年,我國光伏發電新增裝機容量逐年增加
C.2013-2017年,我國光伏發電新增裝機容量的平均值約為2500萬千瓦
D.2017年我國光伏發電新增裝機容量大約占當年累計裝機容量的40%
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,點A的坐標為(2,1),如果將線段OA繞點O逆時針方向旋轉90°,那么點A的對應點的坐標為( )
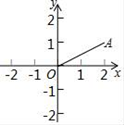
A. (﹣1,2) B. (﹣2,1) C. (1,﹣2) D. (2,﹣1)
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,已知:拋物線![]() 交x軸于A,C兩點,交y軸于點B,且OB=2CO.
交x軸于A,C兩點,交y軸于點B,且OB=2CO.
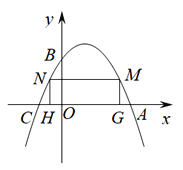
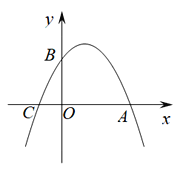
(1)求二次函數解析式;
(2)在二次函數圖象位于x軸上方部分有兩個動點M、N,且點N在點M的左側,過M、N作x軸的垂線交x軸于點G、H兩點,當四邊形MNHG為矩形時,求該矩形周長的最大值;
(3) 拋物線對稱軸上是否存在點P,使得△ABP為直角三角形?若存在,請直接寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知在菱形ABCD中,AB=4,∠BAD=120°,點P是直線AB上任意一點,聯結PC,在∠PCD內部作射線CQ與對角線BD交于點Q(與B、D不重合),且∠PCQ=30°.
(1)如圖,當點P在邊AB上時,如果BP=3,求線段PC的長;
(2)當點P在射線BA上時,設![]() ,求y關于
,求y關于![]() 的函數解析式及定義域;
的函數解析式及定義域;
(3)聯結PQ,直線PQ與直線BC交于點E,如果![]() 與
與![]() 相似,求線段BP的長.
相似,求線段BP的長.
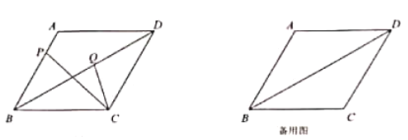
查看答案和解析>>
科目: 來源: 題型:
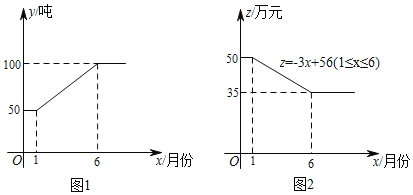
【題目】隨著技術的發展進步,某公司2018年采用的新型原料生產產品.這種新型原料的用量y(噸)與月份x之間的關系如圖1所示,每噸新型原料所生產的產品的售價z(萬元)與月份x之間的關系如圖2所示.已知將每噸這種新型原料加工成的產品的成本為20萬元.
(1)求出該公司這種新型原料的用量y(噸)與月份x之間的函數關系式;
(2)若該公司利用新型原料所生產的產品當月都全部銷售,求哪個月利潤最大,最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com