
科目: 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c與x軸交于A(1,0),B(﹣3,0)兩點.

(1)求該拋物線的解析式;
(2)設(1)中的拋物線交y軸與C點,在該拋物線的對稱軸上是否存在點Q,使得△QAC的周長最小?若存在,求出Q點的坐標;若不存在,請說明理由;
(3)在(1)中的拋物線上的第二象限上是否存在一點P,使△PBC的面積最大?若存在,求出點P的坐標及△PBC的面積最大值;若沒有,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D點,O是AB上一點,經過A、D兩點的⊙O分別交AB、AC于點E、F.
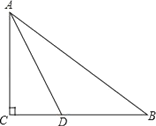
(1)用尺規補全圖形(保留作圖痕跡,不寫作法);
(2)求證:BC與⊙O相切;
(3)當AD=2![]() ,∠CAD=30°時,求劣弧AD的長.
,∠CAD=30°時,求劣弧AD的長.
查看答案和解析>>
科目: 來源: 題型:
【題目】為加快城鄉對接,建設全域美麗鄉村,某地區對A、B兩地間的公路進行改建.如圖,A、B兩地之間有一座山,汽車原來從A地到B地需途徑C地沿折線ACB行駛,現開通隧道后,汽車可直接沿直線AB行駛.已知BC=80千米,∠A=45°,∠B=30°.
(1)開通隧道前,汽車從A地到B地大約要走多少千米?
(2)開通隧道后,汽車從A地到B地大約可以少走多少千米?(結果精確到0.1千米)(參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目: 來源: 題型:
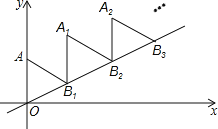
【題目】如圖,放置的△OAB1,△B1A1B2,△B2A2B3,都是邊長為2的等邊三角形,邊AO在Y軸上,點B1、B2、B3都在直線y=![]() x上,則點A2019的坐標為__________________
x上,則點A2019的坐標為__________________
查看答案和解析>>
科目: 來源: 題型:
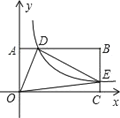
【題目】如圖,在以O為原點的直角坐標系中,矩形OABC的兩邊OC、OA分別在x軸、y軸的正半軸上,反比例函數y=![]() (x>0)與AB相交于點D,與BC相交于點E,若BD=3AD,且△ODE的面積是9,則k=( )
(x>0)與AB相交于點D,與BC相交于點E,若BD=3AD,且△ODE的面積是9,則k=( )
A.![]() B.9C.
B.9C.![]() D.3
D.3
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系![]() 中,對“隔離直線”給出如下定義:點
中,對“隔離直線”給出如下定義:點![]() 是圖形
是圖形![]() 上的任意一點,點
上的任意一點,點![]() 是圖形
是圖形![]() 上的任意一點,若存在直線
上的任意一點,若存在直線![]() :
:![]() 滿足
滿足![]() 且
且![]() ,則稱直線
,則稱直線![]() :
:![]() 是圖形
是圖形![]() 與
與![]() 的“隔離直線”,如圖
的“隔離直線”,如圖![]() ,直線
,直線![]() :
:![]() 是函數
是函數![]() 的圖像與正方形
的圖像與正方形![]() 的一條“隔離直線”.
的一條“隔離直線”.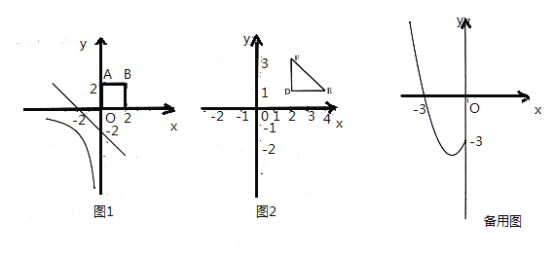
(1)在直線①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,是圖
中,是圖![]() 函數
函數![]() 的圖像與正方形
的圖像與正方形![]() 的“隔離直線”的為 .
的“隔離直線”的為 .
(2)如圖![]() ,第一象限的等腰直角三角形
,第一象限的等腰直角三角形![]() 的兩腰分別與坐標軸平行,直角頂點
的兩腰分別與坐標軸平行,直角頂點![]() 的坐標是
的坐標是![]() ,⊙O的半徑為
,⊙O的半徑為![]() ,是否存在
,是否存在![]() 與⊙O的“隔離直線”?若存在,求出此“隔離直線”的表達式:若不存在,請說明理由;
與⊙O的“隔離直線”?若存在,求出此“隔離直線”的表達式:若不存在,請說明理由;
(3)正方形![]() 的一邊在
的一邊在![]() 軸上,其它三邊都在
軸上,其它三邊都在![]() 軸的左側,點
軸的左側,點![]() 是此正方形的中心,若存在直線
是此正方形的中心,若存在直線![]() 是函數
是函數![]() 的圖像與正方形
的圖像與正方形![]() 的“隔離直線”,請直接寫出
的“隔離直線”,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,二次函數![]() (其中
(其中![]() )的圖像與
)的圖像與![]() 軸分別交于點
軸分別交于點![]() 、
、![]() (點
(點![]() 位于
位于![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,過
,過![]() 點作
點作![]() 軸的平行線
軸的平行線![]() 交二次函數圖于點
交二次函數圖于點![]() .
.

(1)當![]() 時,求
時,求![]() 、
、![]() 兩點的坐標;
兩點的坐標;
(2)過點![]() 作射線
作射線![]() 交二次函數的圖像與點
交二次函數的圖像與點![]() ,使得
,使得![]() ,求
,求![]() 點的坐標(用含
點的坐標(用含![]() 的式子表示)
的式子表示)
(3)在第![]() 問的條件下,二次函數
問的條件下,二次函數![]() 的頂點為
的頂點為![]() ,過點
,過點![]() 、
、![]() 作直線與
作直線與![]() 軸于點
軸于點![]() ,試求出以
,試求出以![]() 、
、![]() 、
、![]() 的長度為三邊長的三角形的面積(用含
的長度為三邊長的三角形的面積(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,已知BC⊥AC,圓心O在AC上,點M與點C分別是AC與⊙O的交點,點D是MB與⊙O的交點,點P是AD延長線與BC的交點,且ADAO=AMAP.
(1)連接OP,證明:△ADM∽△APO;
(2)證明:PD是ΘO的切線;
(3)若AD=24,AM=MC,求![]() 的值.
的值.
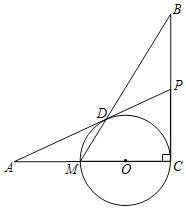
查看答案和解析>>
科目: 來源: 題型:
【題目】為迎接![]() 年中、日、韓三國青少年橄欖球比賽,南雅中學計劃對面積為
年中、日、韓三國青少年橄欖球比賽,南雅中學計劃對面積為![]() 運動場進行塑膠改造.經投標,由甲、乙兩個工程隊來完成,已知甲隊每天能改造的面積是乙隊每天能改造面積的
運動場進行塑膠改造.經投標,由甲、乙兩個工程隊來完成,已知甲隊每天能改造的面積是乙隊每天能改造面積的![]() 倍,并且在獨立完成面積為
倍,并且在獨立完成面積為![]() 的改造時,甲隊比乙隊少用
的改造時,甲隊比乙隊少用![]() 天.
天.
(1)求甲、乙兩工程隊每天能完成塑膠改造的面積;
(2)設甲工程隊施工![]() 天,乙工程隊施工
天,乙工程隊施工![]() 天,剛好完成改造任務,求
天,剛好完成改造任務,求![]() 與
與![]() 的函數解析式;
的函數解析式;
(3)若甲隊每天改造費用是![]() 萬元,乙隊每天改造費用是
萬元,乙隊每天改造費用是![]() 萬元,且甲、乙兩隊施工的總天數不超過
萬元,且甲、乙兩隊施工的總天數不超過![]() 天,如何安排甲、乙兩隊施工的天數,使施工總費用最低?并求出最低的費用.
天,如何安排甲、乙兩隊施工的天數,使施工總費用最低?并求出最低的費用.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com