相關習題
0 153334 153342 153348 153352 153358 153360 153364 153370 153372 153378 153384 153388 153390 153394 153400 153402 153408 153412 153414 153418 153420 153424 153426 153428 153429 153430 153432 153433 153434 153436 153438 153442 153444 153448 153450 153454 153460 153462 153468 153472 153474 153478 153484 153490 153492 153498 153502 153504 153510 153514 153520 153528 366461
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:填空題
下面圖形:正三角形、正方形、等腰梯形、平行四邊形、圓,從中任取一個圖形一定既是軸對稱圖形,又是中心對稱圖形的概率是 .
查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:填空題
已知a≠0,S
1=2a,
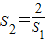
,
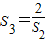
,…,
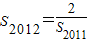
,則S
2012=
(用含a的代數式表示).
查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:填空題
圓柱體內挖去一個與它不等高的圓錐,如其實物圖和其剖面圖所示.錐頂O到AD的距離為1,∠OCD=30°,OC=4,則挖去后該物體的表面積是
.

查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:填空題
如圖,在等腰梯形ABCD中,AD∥BC,BC=4AD=
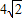
,∠B=45度.直角三角板含45°角的頂點E在邊BC上移動,一直角邊始終經過點A,斜邊與CD交于點F.若△ABE為等腰三角形,則CF的長等于
.
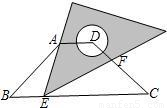
查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:解答題
化簡,求值:
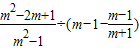
,其中m=
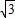
.
查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:解答題
如圖,正方形ABCD和BEFG在直線AB的同側,連接AG、EC,易證AG=EC,現在將正方形BEFG順時針旋轉30°,那么AG=EC還成立嗎?請作出旋轉后的圖形,并證明你的結論.
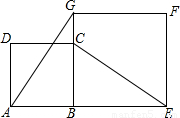
查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:解答題
為更好地宣傳“開車不喝酒,喝酒不開車”的駕車理念,某市一家報社設計了如右的調查問卷(單選).在隨機調查了奉市全部5 000名司機中的部分司機后,統計整理并制作了如下的統計圖:

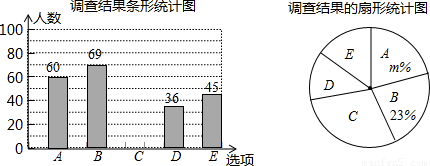
根據以上信息解答下列問題:
(1)補全條形統計圖,并計算扇形統計圖中m=______;
(2)該市支持選項B的司機大約有多少人?
(3)若要從該市支持選項B的司機中隨機選擇100名,給他們發放“請勿酒駕”的提醒標志,則支持該選項的司機小李被選中的概率是多少?
查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:解答題
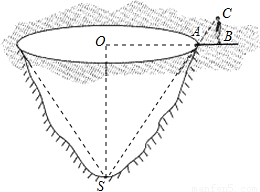
一天,數學課外活動小組的同學們,帶著皮尺去測量某河道因挖沙形成的“圓錐形坑”的深度,來評估這些坑道對河道的影響,如圖是同學們選擇(確保測量過程中無安全隱患)的測量對象,測量方案如下:
①先測出沙坑坑沿的圓周長34.54米;
②甲同學直立于沙坑坑沿的圓周所在的平面上,經過適當調整自己所處的位置,當他位于B時恰好他的視線經過沙坑坑沿圓周上一點A看到坑底S(甲同學的視線起點C與點A,點S三點共線),經測量:AB=1.2米,BC=1.6米.
根據以上測量數據,求圓錐形坑的深度(圓錐的高).(π取3.14,結果精確到0.1米)
查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:解答題
某手機經銷商計劃用61000元購進甲、乙、丙三款品牌手機共60部,設購進甲款手機x部,乙款手機y部,丙款手機z部,三款手機的進價及銷售利潤如下表:
| 手機型號 | 甲 | 乙 | 丙 |
| 進價(元/部) | 900 | 1200 | 1100 |
| 利潤(元/部) | 300 | 400 | 200 |
(1)若只購進兩款手機,恰好用了61000元,請你設計出進貨方案;
(2)求y與x之間的函數關系式;
(3)根據市場需求,每款手機至少購進10部,且所購手機全部售出需支出各種費用共1200元.請你設計出所購手機全部售出可獲得最大利潤的進貨方案.
查看答案和解析>>
科目:
來源:2013年湖北省荊州市中考數學模擬試卷(六)(解析版)
題型:解答題

如圖,已知反比例函數

在第一象限內的圖象經過矩形OABC對角線的交點M,分別與AB、BC相交于點D、E.
(1)用含m的代數式表示四邊形ODBE的面積;
(2)若y關于x的函數y=(2m-1)x
2-2(m+1)x+m+3的圖象與x軸只有一個交點,求四邊形ODBE的面積.
查看答案和解析>>


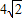 ,∠B=45度.直角三角板含45°角的頂點E在邊BC上移動,一直角邊始終經過點A,斜邊與CD交于點F.若△ABE為等腰三角形,則CF的長等于 .
,∠B=45度.直角三角板含45°角的頂點E在邊BC上移動,一直角邊始終經過點A,斜邊與CD交于點F.若△ABE為等腰三角形,則CF的長等于 .



 一天,數學課外活動小組的同學們,帶著皮尺去測量某河道因挖沙形成的“圓錐形坑”的深度,來評估這些坑道對河道的影響,如圖是同學們選擇(確保測量過程中無安全隱患)的測量對象,測量方案如下:
一天,數學課外活動小組的同學們,帶著皮尺去測量某河道因挖沙形成的“圓錐形坑”的深度,來評估這些坑道對河道的影響,如圖是同學們選擇(確保測量過程中無安全隱患)的測量對象,測量方案如下: 如圖,已知反比例函數
如圖,已知反比例函數 在第一象限內的圖象經過矩形OABC對角線的交點M,分別與AB、BC相交于點D、E.
在第一象限內的圖象經過矩形OABC對角線的交點M,分別與AB、BC相交于點D、E.