日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

如果某中學生的步行速度是每小時6km，他家距離學校3km,學校要求早晨7:30前到校，則他最晚       從家出發才能不遲到.

長方體的底面邊長分別為3cm 和1cm，高為6cm．如果用一根細線從點A開始經過4個側面纏繞一圈到達點B，那么所用細線最短需要__________cm.

用棋子擺成如圖所示的“T”字圖案．擺成第一個“T”字需要5個棋子，第二個圖案需8個棋子；按這樣的規律擺下去，第n個需_______個棋子．

解不等式，并將解集在數軸上表示出來，寫出它的正整數解

先化簡，再求值：，其中．

為了美化環境，在一塊正方形空地上分別種植四種不同的花草.現將這塊空地按下列要求分成四塊：⑴分割后的整個圖形必須是軸對稱圖形；⑵四塊圖形形狀相同；⑶四塊圖形面積相等.現已有兩種不同的分法：⑴分別作兩條對角線（如圖中的圖1）；⑵過一條邊的四等分點作這邊的垂線段（圖2）（圖2中兩個圖形的分割看作同一方法）．請你按照上述三個要求，分別在下面兩個正方形中給出另外兩種不同的分割方法．（正確畫圖，不寫畫法）

近期以來，大蒜和綠豆的市場價格離奇攀升，網民戲稱為“蒜你狠”、“豆你玩”．以綠豆為例，5月上旬某市綠豆的市場價已達16元/千克．市政府決定采取價格臨時干預措施，調進綠豆以平抑市場價格．經市場調研預測，該市每調進100噸綠豆，市場價格就下降1元/千克．為了既能平抑綠豆的市場價格，又要保護豆農的生產積極性，綠豆的市場價格控制在8元/千克到10元/千克之間（含8元/千克和10元/千克）．問調進綠豆的噸數應在什么范圍內為宜？

描述證明：海寶在研究數學問題時發現了一個有趣的現象：

1.請你用數學表達式寫出海寶發現的這個有趣的現象；

2.請你證明海寶發現的這個有趣現象.

1.觀察與發現：

在一次數學課堂上，老師把三角形紙片ABC(AB＞AC)沿過A點的直線折疊，使得AC落在AB邊上，折痕為AD，展開紙片(如圖①)；再次折疊該三角形紙片，使點A和點D重合，折痕為EF，展平紙片后得到△AEF(如圖②)．有同學說此時的△AEF是等腰三角形，你同意嗎？請說明理由．

2.實踐與運用

將矩形紙片ABCD沿過點B的直線折疊，使點A落在BC邊上的點F處，折痕為BE(如圖③)；再沿過點E的直線折疊，使點D落在BE上的點處，折痕為EG(如圖④)；再展平紙片(如圖⑤)．試問：圖⑤中∠的大小是多少？(直接回答，不用說明理由)．

『問題情境』勾股定理是一條古老的數學定理，它有多種證明方法，我國漢代數學家趙爽根據弦圖，利用面積法進行了證明．著名數學家華羅庚曾提出把“數形關系”(勾股定理)帶到其他星球，作為地球人與其它星球“人”進行第一次“談話”的語言．

『定理表述』請你根據圖1中的直角三角形敘述勾股定理(用文字及符號語言敘述)．

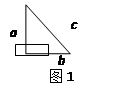
『嘗試證明』以圖1中的直角三角形為基礎，可以構造出以a、b為底，以a＋b為高的直角梯形(如圖2)，請你利用圖2，驗證勾股定理．

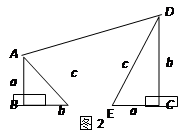
『知識拓展』利用圖2中的直角梯形，我們可以證明＜．其證明步驟如下：

∵BC＝a＋b，AD＝         ，

又在直角梯形ABCD中，BC     AD(填大小關系)，

即                     ．

∴＜．