
科目: 來源: 題型:
甲、乙、丙、丁四位同學圍成一圈依序循環報數,規定:
①甲、乙、丙、丁首次報出的數依次為1、2、3、4,接著甲報5、乙報6……按此規律,后一位同學報出的數比前一位同學報出的數大1,當報到的數是51時,報數結束;
②若報出的數為3的倍數,則報該數的同學需拍手一次.在此過程中,丙同學需要拍手的次數為____________.
查看答案和解析>>
科目: 來源: 題型:
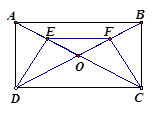
)如圖,已知矩形ABCD的對角線AC、BD
相交于點O,E、F分別是OA、OB的中點.
1.求證:△ADE≌△BCF;
2.若AD=4cm,AB=8cm,求OF的長.
查看答案和解析>>
科目: 來源: 題型:閱讀理解
先閱讀下面兩個簡單的推理,然后解決問題:
①對于任意實數x,
∵x2≥0 ,
∴x2+1>0;
②對于任意實數x,
∵(x-![]() )2≥0,
)2≥0,
∴(x-![]() )2+
)2+![]() >0
>0
問題:
1.求證:對于任何實數,均有2x2+4x+3>0
2.先在下面的括號內填上適當的選項,再證明你的結論.
設M=3x2-5x-1,N=2x2-4x-7,則( )
A. M>N B.M<N C.M≥N D.M≤N
查看答案和解析>>
科目: 來源: 題型:
某居民小區一處圓柱形的輸水管道破裂,維修人員為更換管道,需確定管道圓形截面的半徑,下圖是水平放置的破裂管道有水部分的截面.
1.請你用直尺和圓規補全這個輸水管道的圓形截面(不寫作法,保留作圖痕跡);
2.若這個輸水管道有水部分的水面寬AB=18cm,水面最深地方的深度為3cm,
求這個圓形截面的半徑.
查看答案和解析>>
科目: 來源: 題型:
我們已經學過用方差來描述一組數據的離散程度,其實我們還可以用“平均差”來描述一組數據的離散程度。在一組數據x1,x2,…,xn中,各數據與它們的平均數![]() 的差的絕對值的平均數,即T=
的差的絕對值的平均數,即T=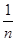 (|x1-
(|x1-![]() |+|x2-
|+|x2-![]() |+…+|xn-
|+…+|xn-![]() |)叫做這組數據的“平均差”,“平均差”也能描述一組數據的離散程度,“平均差”越大說明數據的離散程度越大。
|)叫做這組數據的“平均差”,“平均差”也能描述一組數據的離散程度,“平均差”越大說明數據的離散程度越大。
請你解決下列問題:
1.分別計算下列甲乙兩個樣本數據的“平均差”,并根據計算結果判斷哪個樣本波動較大。
甲:12,13,11,10,14, 乙:10,17,10,13,10
2.分別計算甲、乙兩個樣本數據的方差和標準差,并根據計算結果判斷哪個樣本波動較大.
3.以上的兩種方法判斷的結果是否一致?
查看答案和解析>>
科目: 來源: 題型:閱讀理解
先閱讀,然后解決問題:
已知:一次函數![]() 和反比例函數
和反比例函數![]() ,求這兩個函數圖象在同一坐標系內的交點坐標。
,求這兩個函數圖象在同一坐標系內的交點坐標。
解:解方程-x+2=![]()
去分母,得
-x2+2x=-8
整理得
x2-2x-8=0
解這個方程得:x1=-2 x2=4
經檢驗,x1=-2 x2=4是原方程的根
當x1=-2,y1=4;x2=4,y2=-2
∴交點坐標為(-2,4)和(4,-2)
問題:
1.在同一直角坐標系內,求反比例函數y= 的圖象與一次函數y=x+3的圖象的交點坐標;
的圖象與一次函數y=x+3的圖象的交點坐標;
2.判斷一次函數y=2x-3的圖象與反比例函數y=-![]() 的圖象在同一直角坐標系內有無交點,說明理由.
的圖象在同一直角坐標系內有無交點,說明理由.
查看答案和解析>>
科目: 來源: 題型:
如圖,已知AB是⊙O的直徑,點D、E在⊙O上,且︵AD∶︵DE=3∶5, ︵BE的度數為20°,連接DE并延長交AB的延長線于C,
1.求∠AOD的度數;
2.判斷CE與AB有什么數量關系,并說明理由
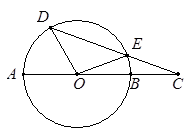
查看答案和解析>>
科目: 來源: 題型:
已知,正方形ABCD,點P在對角線BD上,連接AP、CP(如圖①)
1.求證:AP=CP.
2.將一直角三角板的直角頂點置于點P處并繞點P旋轉,設兩直角邊分別交DC、BC于E、F,
a.若旋轉到圖②位置,使PE與PA在一直線上,求證:PF=PA.
b.若旋轉到圖③位置且PD∶PB=2∶3,求PE∶PF的值.
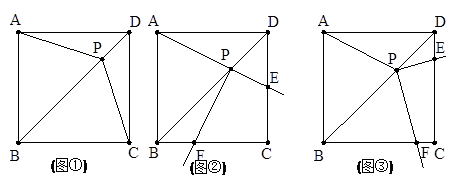
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com