在平面直角坐標系xOy中,拋物線y=-x2+bx+c與x軸交于A、B兩點,與y軸交于點C,頂點為D,過點A的直線與拋物線交于點E,與y軸交于點F,且點B的坐標為(3,0),點E的坐標為(2,3).
(1)求拋物線的解析式;
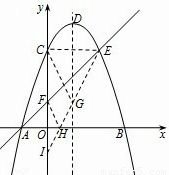
(2)若點G為拋物線對稱軸上的一個動點,H為x軸上一點,當以點C、G、H、F四點所圍成的四邊形的周長最小時,求出這個最小值及點G、H的坐標;
(3)設直線AE與拋物線對稱軸的交點為P,M為直線AE上的任意一點,過點M作MN∥PD交拋物線于點N,以P、D、M、N為頂點的四邊形能否為平行四邊形?若能,請求點M的坐標;若不能,請說明理由.
【答案】
分析:(1)將點B和點E的坐標代入y=-x
2+bx+c,建立二元一次方程組,求出b、c的值即可;
(2)先根據(1)的結論求出A、C的坐標及對稱軸,畫出函數圖象,在y軸的負半軸上取一點I,使得點F點I關于x軸對稱,在x軸上取點H,連接HF、HI、HG、GC、GE、則GF=HI.由待定系數法求出AE的解析式,求出F的坐標,就可以求出CF的值,由勾股定理可以求出EI的值,根據兩點之間線段最短,求出求出EI的解析式就可以求出G、H的坐標,由勾股定理就可以求出最小值;
(3)根據平行四邊形的性質和AE的解析式就可以求出D的坐標,由拋物線的解析式可以求出D的坐標,求出PD的值,可以設出M的坐標(x,x+1)分情況討論當M在線段AE上和在線段AE或EA的延長線上時,分別表示出N點的坐標從而求出結論.
解答:解:(1)∵y=-x
2+bx+c經過(3,0)和(2,3),
∴
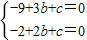
,
解得:
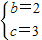
,
∴拋物線的解析式為:y=-x
2+2x+3;
(2)∵y=-x
2+2x+3,
∴y=-(x-1)
2+4,
∴對稱軸為x=1.
當y=0時,-x
2+2x+3=0,
∴x
1=-1,x
2=3,
∴A(-1,0).
當x=0時,y=3,
∴C(0,3)
∴CE=2.OC=3
如圖,在y軸的負半軸上取一點I,使得點F點I關于x軸對稱,在x軸上取點H,連接HF、HI、HG、GC、GE、則GF=HI.
∵拋物線的對稱軸為x=1,
∴點C點E關于對稱軸x=1對稱,
∴CG=EG.
設直線AE的解析式為y=kx+b,由題意,得
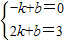
,
解得:
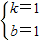
,
∴直線AE的解析式為y=x+1.
當x=0時,y=1,
∴F(0,1),
∴OF=1,CF=2.
∵點F與點I關于x軸對稱,
∴I(0,-1),
∴OI=1,CI=4.
在Rt△CIE中,由勾股定理,得
EI=
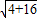
=2
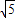
.
∵要使四邊形CFHG的周長最小,而CF是定值,
∴只要使CG+GH+HF最小即可.
∵CG+GH+HF=EG+GH+HI,
∴只有當EI為一條直線時,EG+GH+HI最小.
設EI的解析式為y=k
1x+b
1,由題意,得
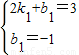
,
解得:
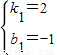
,
∴直線EI的解析式為:y=2x-1,
∵當x=1時,y=1,
∴G(1,1).
∵當y=0時,x

,
∴H(

,0),
∴四邊形CFHG的周長最小值=CF+CG+GH=CF+EI=2+2
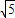
;
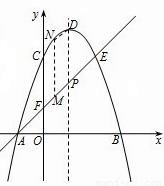
(3)∵y=-x
2+2x+3,
∴y=-(x-1)
2+4,
∴D(1,4)
∴直線AE的解析式為y=x+1.
∴x=1時,y=2,
∴P(1,2),
∴PD=2.
∵四邊形DPMN是平行四邊形,
∴PD=MN=2.
∵點M在AE上,設M(x,x+1),
①當點M在線段AE上時,點N點M的上方,則N(x,x+3),
∵N點在拋物線上,
∴x+3=-x
2+2x+3,
解得:x=0或x=1(舍去)
∴M(0,1).
②當點M在線段AE或EA的延長線上時,點N在M的下方,則N(x,x-1).
∵N點在拋物線上,
∴x-1=-x
2+2x+3,
解得:x=
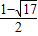
或x=
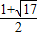
,
∴M(
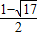
,
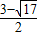
)或(
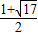
,
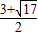
).
∴M的坐標為:M(0,1)或(
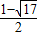
,
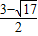
)或(
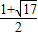
,
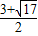
).
點評:本題是一道二次函數的綜合試題,考查了待定系數法求函數的解析式的運用,四邊形周長的最值的運用,軸對稱的性質的運用,數學建模的運用,平行四邊形的性質的運用,分類討論思想的運用,解答本題時求出函數的解析式是關鍵.

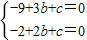 ,
,
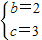 ,
,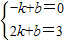 ,
,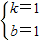 ,
,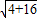 =2
=2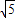 .
.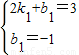 ,
,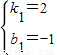 ,
, ,
, ,0),
,0),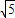 ;
;
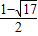 或x=
或x=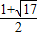 ,
,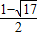 ,
,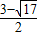 )或(
)或(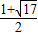 ,
,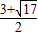 ).
).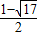 ,
,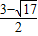 )或(
)或(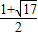 ,
,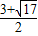 ).
).

 如圖,在平面直角坐標系xOy中,△ABC的A、B兩個頂點在x軸上,頂點C在y軸的負半軸上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面積S△ABC=15,拋物線y=ax2+bx+c(a≠0)經過A、B、C三點.
如圖,在平面直角坐標系xOy中,△ABC的A、B兩個頂點在x軸上,頂點C在y軸的負半軸上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面積S△ABC=15,拋物線y=ax2+bx+c(a≠0)經過A、B、C三點. 如圖,在平面直角坐標系xOy中,A(2,1)、B(4,1)、C(1,3).與△ABC與△ABD全等,則點D坐標為
如圖,在平面直角坐標系xOy中,A(2,1)、B(4,1)、C(1,3).與△ABC與△ABD全等,則點D坐標為