
分析 (1)分兩種情況進行討論:①當∠A為銳角時,如圖1所示;②當∠A為鈍角時,如圖2所示,分別根據角的和差關系求得y關于x的函數表達式,并寫出自變量的取值范圍即可;
(2)當x=60°時,由(1)可得,y=180°-2×60°=60°,得出∠EDF=60°,再根據Rt△BCE中,DE=$\frac{1}{2}$BC,Rt△BCF中,DF=$\frac{1}{2}$BC,可得DE=DF,據此判定△DEF的形狀為等邊三角形;
(3)分兩種情況進行討論:①當∠A為銳角時,如圖1所示;②當∠A為鈍角時,如圖2所示,分別根據△DEF為等腰直角三角形,且DE=DF,得出∠EDF為直角,即y=90,分別運用(1)中的函數解析式即可求得x的值.
解答 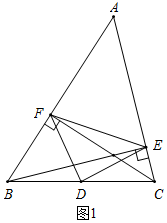 解:(1)①當∠A為銳角時,如圖1所示,
解:(1)①當∠A為銳角時,如圖1所示,
∵BE⊥AC于E,CF⊥AB于F,BD=DC,
∴Rt△BCE中,DE=$\frac{1}{2}$BC=CD,
Rt△BCF中,DF=$\frac{1}{2}$BC=BD,
∴∠BDE=2∠DCE,∠CDF=2∠DBF,
又∵∠BDE+∠CDF-∠EDF=180°,
∴2∠DCE+2∠DBF-∠EDF=180°,
即2(∠DCE+∠DBF)-∠EDF=180°,
∴2(180°-∠A)-∠EDF=180°,
又∵∠BAC=x,∠EDF=y,
∴2(180-x)-y=180,
∴y=2(180-x)-180,
即y=180-2x(0<x<90);
②當∠A為鈍角時,如圖2所示,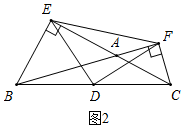
∵BE⊥AC于E,CF⊥AB于F,BD=DC,
∴Rt△BCE中,DE=$\frac{1}{2}$BC=CD,
Rt△BCF中,DF=$\frac{1}{2}$BC=BD,
∴∠BDE=2∠DCE,∠CDF=2∠DBF,
又∵∠BDE+∠CDF+∠EDF=180°,
∴2∠DCE+2∠DBF+∠EDF=180°,
即2(∠DCE+∠DBF)+∠EDF=180°,
∴2(180°-∠A)+∠EDF=180°,
又∵∠BAC=x,∠EDF=y,
∴2(180-x)+y=180,
∴y=180-2(180-x),
即y=2x-180(90<x<180);
綜上所述,y關于x的函數表達式為y=$\left\{\begin{array}{l}{180-2x(0<x<90)}\\{2x-180(90<x<180)}\end{array}\right.$;
(2)當x=60°時,由(1)可得,y=180°-2×60°=60°,
即∠EDF=60°,
又∵Rt△BCE中,DE=$\frac{1}{2}$BC,
Rt△BCF中,DF=$\frac{1}{2}$BC,
∴DE=DF,
∴△DEF的形狀為等邊三角形;
(3)①如圖1,∵△DEF為等腰直角三角形,且DE=DF,
∴∠EDF為直角,
即y=90,
此時,90=180-2x,
解得x=45,
故x的值為45;
②如圖2,∵△DEF為等腰直角三角形,且DE=DF,
∴∠EDF為直角,
即y=90,
此時,90=2x-180,
解得x=135,
故x的值為135;
綜上所述,若△DEF為等腰直角三角形,x的值為45或135.
點評 本題屬于三角形綜合題,主要考查了直角三角形的性質,等腰三角形的性質以及等邊三角形的判定的綜合應用,解決問題的關鍵是畫出相應的圖形,運用分類討論思想,根據角的和差關系進行求解.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
| A. | 單項式$\frac{3}{2}π{x^2}y$的系數是$\frac{3}{2}$ | |
| B. | 若AB=BC,則點B是線段AC的中點 | |
| C. | 3和5是同類項 | |
| D. | 同一平面內,過一點有且只有一條直線與已知直線平行 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
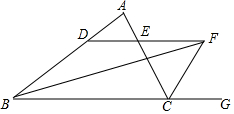 如圖,∠ABC的平分線BF與△ABC中∠ACB的相鄰外角∠ACG的平分線CF相交于點F,過F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的長.
如圖,∠ABC的平分線BF與△ABC中∠ACB的相鄰外角∠ACG的平分線CF相交于點F,過F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的長.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
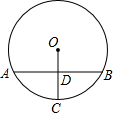 如圖,⊙O的弦AB與半徑OC垂直,點D為垂足,OD=DC,AB=2$\sqrt{3}$,點E在⊙O上,∠EOA=30°,則△EOC的面積為1或2.
如圖,⊙O的弦AB與半徑OC垂直,點D為垂足,OD=DC,AB=2$\sqrt{3}$,點E在⊙O上,∠EOA=30°,則△EOC的面積為1或2.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 閱讀下面材料:下面是“作角的平分線”的尺規作圖過程.
閱讀下面材料:下面是“作角的平分線”的尺規作圖過程.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com