
分析 將a+b=3,ab=1代入原式=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$即可得;
由已知等式可得a2+2ab+b2=20 ①,${a}^{2}-2ab+{b}^{2}=4\\;\$ ②,①-②即可得.
解答 解:當a+b=3,ab=1時,
原式=$\frac{{a}^{2}+{b}^{2}}{ab}$
=$\frac{(a+b)^{2}-2ab}{ab}$
=$\frac{{3}^{2}-2}{1}$
=7;
∵(a+b)2=20,(a-b)2=4,
∴a2+2ab+b2=20 ①,
${a}^{2}-2ab+{b}^{2}=4\\;\$ ②,
①-②,得:4ab=16,
∴ab=4,
故答案為:7,4.
點評 本題主要考查分式的化簡求值,熟練掌握完全平方公式是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
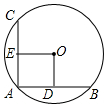 如圖,在⊙O中,相等的弦AB、AC互相垂直,OE⊥AC于E,OD⊥AB于D,則四邊形OEAD為( )
如圖,在⊙O中,相等的弦AB、AC互相垂直,OE⊥AC于E,OD⊥AB于D,則四邊形OEAD為( )| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四邊形 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
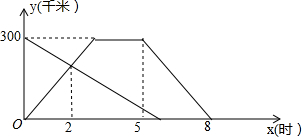 甲、乙兩車分別從A、B兩地同時出發相向而行,并以各自的速度勻速行駛,甲車到達B地后,停留一段時間,然后按原路原速度返回A地;乙車到達A地立即停止行駛.甲、乙兩車和A地的距離y(千米)與甲車出發時間x(時)的函數圖象如圖所示.
甲、乙兩車分別從A、B兩地同時出發相向而行,并以各自的速度勻速行駛,甲車到達B地后,停留一段時間,然后按原路原速度返回A地;乙車到達A地立即停止行駛.甲、乙兩車和A地的距離y(千米)與甲車出發時間x(時)的函數圖象如圖所示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com