【題目】在平面直角坐標系xOy中，函數y1＝x（x＜m）的圖象與函數y2＝x2（x≥m）的圖象組成圖形G．對于任意實數n，過點P（0，n）且與x軸平行的直線總與圖形G有公共點，寫出一個滿足條件的實數m的值為_____（寫出一個即可）．
科目：初中數學 來源： 題型：
【題目】五一期間，樂樂與小佳兩個人打算騎共享單車騎行出游，兩人打開手機
進行選擇，已知附近共有3種品牌的4輛車，其中
品牌有2輛，
品牌和
品牌各有1輛，手機上無法識別品牌，且有人選中車后其他人無法再選．
（1）若樂樂首先選擇，求樂樂選中品牌單車的概率；
（2）請用畫樹狀圖或列表的方法求樂樂和小佳選中同一品牌單車的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一筆總額為
元的獎金，分為一等獎、二等獎和三等獎，獎金金額均為整數，每個一等獎的獎金是每個二等獎獎金的兩倍，每個二等獎的獎金是每個三等獎獎金的兩倍，若把這筆獎金發給
個人，評一、二、三等獎的人數分別為
，且
，那么三等獎的獎金金額是_______元．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果
的兩個端點
分別在
的兩邊上(不與點
重合)，并且除端點外的所有點都在的內部，則稱是的“連角弧”．
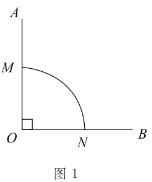
(1)圖1中，是直角，是以為圓心，半徑為1的“連角弧”．
①圖中的長是______，并在圖中再作一條以
為端點、長度相同的“連角弧”；
②以為端點，弧長最長的“連角弧”的長度是_______．
(2)如圖2，在平面直角坐標系
中，點
，點
在
軸正半軸上，若是半圓，也是的“連角弧”，求
的取值范圍．
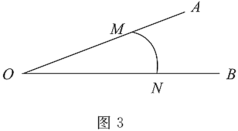
(3)如圖3，已知點分別在射線
上，
是的“連角弧”，且所在圓的半徑為
，直接寫出的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】北京某超市按月訂購一種酸奶，每天的進貨量相同．根據往年的銷售經驗，每天需求量與當天最高氣溫（單位：℃）有關．為了確定今年六月份的酸奶訂購計劃，對前三年六月份的最高氣溫及該酸奶需求量數據進行了整理、描述和分析，下面給出了部分信息．
a．酸奶每天需求量與當天最高氣溫關系如表：
最高氣溫t（單位：℃） | 20≤t＜25 | 25≤t＜30 | 30≤t≤40 |
酸奶需求量（單位：瓶/天） | 300 | 400 | 600 |
b.2017年6月最高氣溫數據的頻數分布統計表如表（不完整）：
2017年6月最高氣溫數據的頻數分布表：
分組 | 頻數 | 頻率 |
20≤t＜25 | 3 | |
25≤t＜30 | m | 0.20 |
30≤t＜35 | 14 | |
35≤t≤40 | 0.23 | |
合計 | 30 | 1.00 |
c.2018年6月最高氣溫數據的頻數分布直方圖如圖：
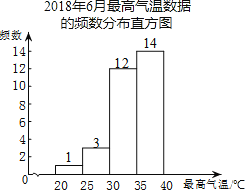
d.2019年6月最高氣溫數據如下（未按日期順序）：
25 26 28 29 29 30 31 31 31 32 32 32 32 32 32
33 33 33 33 33 34 34 34 35 35 35 35 36 36 36
根據以上信息，回答下列問題：
（1）m的值為 ；
（2）2019年6月最高氣溫數據的眾數為 ，中位數為 ；
（3
（4）已知該酸奶進貨成本每瓶4元，售價每瓶6元，未售出的酸奶降價處理，以每瓶2元的價格當天全部處理完．
①2019年6月這種酸奶每天的進貨量為500瓶，則此月這種酸奶的利潤為 元；
②根據以上信息，預估2020年6月這種酸奶訂購的進貨量不合理的為 ．
A．550瓶/天
B．600瓶/天
C．380瓶/天
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】新冠肺炎疫情暴發后，一場同時間賽跑、與病魔較量的戰役隨即打響．在疫情防控一線，除了廣大醫務工作者義無反顧、日夜奮戰之外，在另一條戰線上，科研人員也在加班加點、緊急攻關．全國科技戰線積極響應黨中央號召，科技、衛健等12個部門組成科研攻關組，短短一個月的時間內就取得了積極進展．3月13日0﹣24時，31個省（自治區、直轄市）和新疆生產建設兵團新增確診病例11例（數據不含港澳臺），新增疑似病例17例（數據不含港澳臺）．如圖是根據國家衛健委關于新型冠狀病毒肺炎通報的數據（數據不含港澳臺）繪制的統計圖：
根據以上信息，回答下列問題：
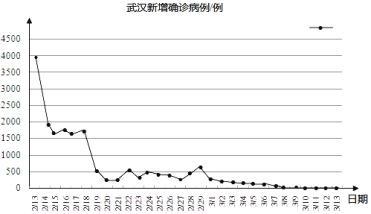
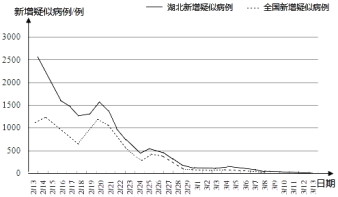
（1）下列推斷合理的是_______．
①2月15日武漢新增確診病例約為1500例；
②從2月23日起到3月13日止，武漢每日新增確診病例都在500例以下；
③從2月23日起到3月13日止，全國每日新增疑似病例逐漸減少．
④3月13日湖北新增疑似病例不超過17例．
（2）結合本題的信息及當前防疫形勢，說說你的感受．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：在平面直角坐標系xOy中，函數y＝
（n≠0，x＞0）的圖象過點A（3，2），與直線l：y＝kx+b交于點C，直線l與y軸交于點B（0，﹣1）．
（1）求n、b的值；
（2）橫、縱坐標都是整數的點叫做整點．記函數y＝（n≠0，x＞0）的圖象在點A，C之間的部分與線段BA，BC圍成的區域（不含邊界）為W．
①當直線l過點（2，0）時，直接寫出區域W內的整點個數，并寫出區域W內的整點的坐標；
②若區域W內的整點不少于5個，結合函數圖象，求k的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線
與
軸交于
、
兩點，對稱軸與軸交于點
，點
，點
，點
是平面內一動點，且滿足
，
是線段
的中點，連結
．則線段的最大值是（ ）．
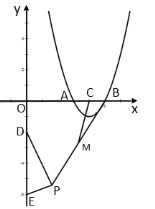
A.3B.
C.
D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
