
【題目】新冠肺炎疫情暴發后,一場同時間賽跑、與病魔較量的戰役隨即打響.在疫情防控一線,除了廣大醫務工作者義無反顧、日夜奮戰之外,在另一條戰線上,科研人員也在加班加點、緊急攻關.全國科技戰線積極響應黨中央號召,科技、衛健等12個部門組成科研攻關組,短短一個月的時間內就取得了積極進展.3月13日0﹣24時,31個省(自治區、直轄市)和新疆生產建設兵團新增確診病例11例(數據不含港澳臺),新增疑似病例17例(數據不含港澳臺).如圖是根據國家衛健委關于新型冠狀病毒肺炎通報的數據(數據不含港澳臺)繪制的統計圖:
根據以上信息,回答下列問題:
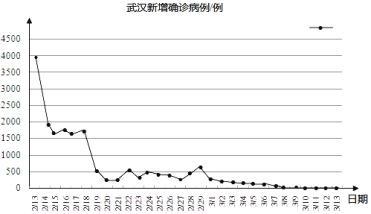
(1)下列推斷合理的是_______.
①2月15日武漢新增確診病例約為1500例;
②從2月23日起到3月13日止,武漢每日新增確診病例都在500例以下;
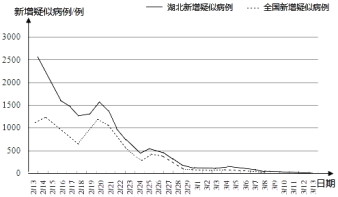
③從2月23日起到3月13日止,全國每日新增疑似病例逐漸減少.
④3月13日湖北新增疑似病例不超過17例.
(2)結合本題的信息及當前防疫形勢,說說你的感受.
 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案科目:初中數學 來源: 題型:
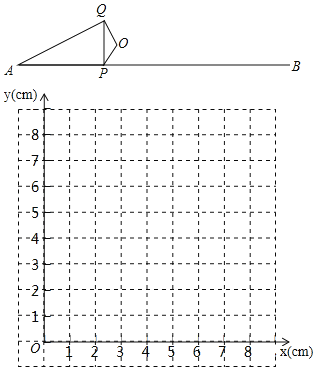
【題目】如圖,P是線段AB上的一點,AB=6cm,O是AB外一定點.連接OP,將OP繞點O順時針旋轉120°得OQ,連接PQ,AQ.小明根據學習函數的經驗,對線段AP,PQ,AQ的長度之間的關系進行了探究.
下面是小明的探究過程,請補充完整:
(1)對于點P在AB上的不同位置,畫圖、測量,得到了線段AP,PQ,AQ的長度(單位:cm)的幾組值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP,PQ,AQ的長度這三個量中,確定 的長度是自變量, 的長度和 的長度都是這個自變量的函數;/span>
(2)在同一平面直角坐標系xOy中,畫出(1)中所確定的函數的圖象;
(3)結合函數圖象,解決問題:當AQ=PQ時,線段AP的長度約為 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班甲、乙、丙三名同學20天的體溫數據記錄如下表:
甲的體溫 | 乙的體溫 | 丙的體溫 | ||||||||||||
溫度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 溫度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 溫度(℃) | 36.1 | 36.4 | 36.5 | 36.8 |
頻數 | 5 | 5 | 5 | 5 | 頻數 | 6 | 4 | 4 | 6 | 頻數 | 4 | 6 | 6 | 4 |
則在這20天中,甲、乙、丙三名同學的體溫情況最穩定的是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,函數y1=x(x<m)的圖象與函數y2=x2(x≥m)的圖象組成圖形G.對于任意實數n,過點P(0,n)且與x軸平行的直線總與圖形G有公共點,寫出一個滿足條件的實數m的值為_____(寫出一個即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=ax2+4ax+b(a>0)的頂點A在x軸上,與y軸交于點B.
(1)用含a的代數式表示b;
(2)若∠BAO=45°,求a的值;
(3)橫、縱坐標都是整數的點叫做整點.若拋物線在點A,B之間的部分與線段AB所圍成的區域(不含邊界)內恰好沒有整點,結合函數的圖象,直接寫出a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=x2﹣2mx+m﹣4與x軸交于點A,B(點A在點B的左側),與y軸交于點C(0,﹣3).
(1)求m的值;
(2)若一次函數y=kx+5(k≠0)的圖象經過點A,求k的值;
(3)將二次函數的圖象在點B,C間的部分(含點B和點C)向左平移n(n>0)個單位后得到的圖象記為G,同時將(2)中得到的直線y=kx+5(k≠0)向上平移n個單位,當平移后的直線與圖象G有公共點時,請結合圖象直接寫出n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
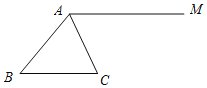
【題目】如圖,AM∥BC,且AC平分∠BAM.
(1)用尺規作∠ABC的平分線BD交AM于點D,連接CD.(只保留作圖痕跡,不寫作法)
(2)求證:四邊形ABCD是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知∠MON=α,A為射線OM上一定點,OA=5,B為射線ON上一動點,連接AB,滿足∠OAB,∠OBA均為銳角.點C在線段OB上(與點O,B不重合),滿足AC=AB,點C關于直線OM的對稱點為D,連接AD,OD.
(1)依題意補全圖1;
(2)求∠BAD的度數(用含α的代數式表示);
(3)若tanα=![]() ,點P在OA的延長線上,滿足AP=OC,連接BP,寫出一個AB的值,使得BP∥OD,并證明.
,點P在OA的延長線上,滿足AP=OC,連接BP,寫出一個AB的值,使得BP∥OD,并證明.
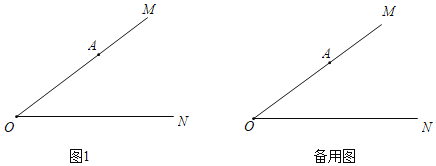
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在“愛護地球,綠化祖國”的活動中,組織同學開展植樹造林活動,為了了解同學的植樹情況,學校抽查了初一年級所有同學的植樹情況(初一年級共有兩個班),并將調查數據整理繪制成如下所示的部分數據尚不完整的統計圖表.下面有四個推斷:
初一年級植樹情況統計表 | |||||
棵樹/棵 | 1 | 2 | 3 | 4 | 5 |
人數 | 7 | 33 | a | 12 | 3 |
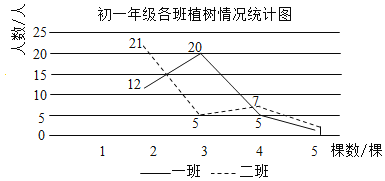
①a的值為20;
②初一年級共有80人;
③一班植樹棵樹的眾數是3;
④二班植樹棵樹的是中位數2.
其中合理的是( )
A.①③B.②④C.②③D.②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com