
【題目】如圖1, O為正方形ABCD的中心,分別延長OA,OD到點F,E,使OF=2OA,OE=2OD,連接EF,將△FOE繞點O按逆時針方向旋轉角α得到△FOE,連接AE,BF(如圖2).
(1)探究AE與BF的數量關系,并給予證明;
(2)當α=30°時,求證: △AOE為直角三角形.

【答案】(1)AE=BF,理由見解析;(2)證明見解析.
【解析】試題分析:(1)利用旋轉不變量找到相等的角和線段,證得△E′AO≌△F′BO后即可證得結論;
(2)利用已知角,得出∠GAE′=∠GE′A=30°,從而證明直角三角形.
試題解析:(1)證明:∵O為正方形ABCD的中心,
∴OA=OD,
∵OF=2OA,OE=2OD,
∴OE=OF,
∵將△EOF繞點O逆時針旋轉α角得到△E′OF′,
∴OE′=OF′,
∵∠F′OB=∠E′OA,OA=OB,
在△E′AO和△F′BO中,
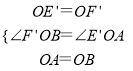 ,
,
∴△E′AO≌△F′BO,
∴AE′=BF′;
(2)證明:∵取OE′中點G,連接AG,
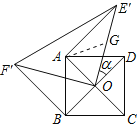
∵∠AOD=90°,α=30°,
∴∠E′OA=90°-α=60°,
∵OE′=2OA,
∴OA=OG,
∴∠E′OA=∠AGO=∠OAG=60°,
∴AG=GE′,
∴∠GAE′=∠GE′A=30°,
∴∠E′AO=90°,
∴△AOE′為直角三角形.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案科目:初中數學 來源: 題型:
【題目】某中學為了響應國家發展足球的戰略方針,激發學生對足球的興趣,特舉辦全員參與的“足球比賽”,賽后,全校隨機抽查部分學生,其成績(百分制)整理分成5組,并制成如下頻數分布表和扇形統計圖,請根據所提供的信息解答下列問題:
成績頻數分布表
組別 | 成績(分) | 頻數 |
A | 50≤x<60 | 6 |
B | 60≤x<70 | m |
C | 70≤x<80 | 20 |
D | 80≤x<90 | 36 |
E | 90≤x<100 | n |

(1)頻數分布表中的m= , n=;
(2)樣本中位數所在成績的級別是 , 扇形統計圖中,E組所對應的扇形圓心角的度數是;
(3)若該校共有2000名學生,請你估計體育綜合測試成績不少于80分的大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分類
﹣3,0.45, ![]() ,0,9,﹣1,﹣1
,0,9,﹣1,﹣1![]() ,10,﹣3.14
,10,﹣3.14
(1)正整數:{ …}
(2)負整數:{ …}
(3)整數:{ …}
(4)分數:{ …}.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形ABCD中,動點F,E分別以相同的速度從D,C兩點同時出發向C和B運動(任何一個點到達即停止),過點P作PM∥CD交BC于M點,PN∥BC交CD于N點,連接MN,在運動過程中, ①AE和BF的位置關系為;
②線段MN的最小值為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:[x]表示不大于x的最大整數,(x)表示不小于x的最小整數,[x)表示最接近x的整數(x≠n+0.5,n為整數),例如:[2.3]=2,(2.3)=3,[2.3)=2.當﹣1<x<1時,化簡 [x]+(x)+[x)的結果是__________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果∠A和∠B互補,且∠A>∠B,給出下列四個式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序號)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
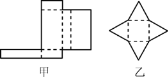
【題目】觀察圖,回答下列問題:
(1)甲、乙兩圖分別能折成什么幾何體?簡述它們的特征;
(2)設幾何體的面數為F,頂點數為V,棱數為E,請計算(1)中兩個幾何體的F+V-E的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小黃準備給長8m,寬6m的長方形客廳鋪設瓷磚,現將其劃分成一個長方形ABCD區域Ⅰ(陰影部分)和一個環形區域Ⅱ(空白部分),其中區域Ⅰ用甲、乙、丙三種瓷磚鋪設,且滿足PQ∥AD,如圖所示.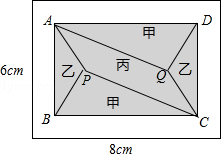
(1)若區域Ⅰ的三種瓷磚均價為300元/m2 , 面積為S(m2),區域Ⅱ的瓷磚均價為200元/m2 , 且兩區域的瓷磚總價為不超過12000元,求S的最大值;
(2)若區域Ⅰ滿足AB:BC=2:3,區域Ⅱ四周寬度相等
①求AB,BC的長;
②若甲、丙兩瓷磚單價之和為300元/m2 , 乙、丙瓷磚單價之比為5:3,且區域Ⅰ的三種瓷磚總價為4800元,求丙瓷磚單價的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com