
【題目】一個不透明的袋中裝有紅、黃、白三種顏色球共100個,它們除顏色外都相同,其中黃球個數是白球個數的2倍少5個.已知從袋中摸出一個球是紅球的概率是 ![]() .
.
(1)求袋中紅球的個數;
(2)求從袋中摸出一個球是白球的概率;
(3)取走10個球(其中沒有紅球)后,求從剩余的球中摸出一個球是紅球的概率.
【答案】
(1)解:根據題意得:
100× ![]() ,
,
答:紅球有30個
(2)解:設白球有x個,則黃球有(2x﹣5)個,
根據題意得x+2x﹣5=100﹣30
解得x=25.
所以摸出一個球是白球的概率P= ![]() =
= ![]()
(3)解:因為取走10個球后,還剩90個球,其中紅球的個數沒有變化,
所以從剩余的球中摸出一個球是紅球的概率 ![]() =
= ![]()
【解析】(1)根據紅、黃、白三種顏色球共有的個數乘以紅球的概率即可;(2)設白球有x個,得出黃球有(2x﹣5)個,根據題意列出方程,求出白球的個數,再除以總的球數即可;(3)先求出取走10個球后,還剩的球數,再根據紅球的個數,除以還剩的球數即可.
【考點精析】認真審題,首先需要了解概率公式(一般地,如果在一次試驗中,有n種可能的結果,并且它們發生的可能性都相等,事件A包含其中的m中結果,那么事件A發生的概率為P(A)=m/n).


科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AB>BC,按以下步驟作圖:以A為圓心,小于AD的長為半徑畫弧,分別交AB、CD于E、F;再分別以E、F為圓心,大于 ![]() EF的長半徑畫弧,兩弧交于點G;作射線AG交CD于點H.則下列結論:①AG平分∠DAB,②CH=
EF的長半徑畫弧,兩弧交于點G;作射線AG交CD于點H.則下列結論:①AG平分∠DAB,②CH= ![]() DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH= ![]() S四邊形ABCH .
S四邊形ABCH .
其中正確的有( )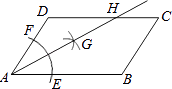
A.①②③
B.①③④
C.②④
D.①③
查看答案和解析>>
科目:初中數學 來源: 題型:
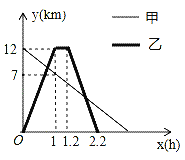
【題目】某地植物園從正門到側門有一條小路,甲徒步從正門出發勻速走向側門,乙與甲同時出發,騎自行車從側門勻速前往正門到達正門后休息0.2小時,然后按原路原速勻速返回側門,圖中折線分別表示甲、乙到側門的距離y(km)與出發時間x(h)之間的函數關系圖象,根據圖象信息解答下列問題:
(1)求甲到側門的距離y與x之間的函數關系式;
(2)求甲、乙第一次相遇時到側門的距離.
(3)求甲、乙第二次相遇的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,經過原點的拋物線y=﹣x2+2mx(m>0)與x軸的另一個交點為A.過點P(1,m)作直線PM⊥x軸于點M,交拋物線于點B.記點B關于拋物線對稱軸的對稱點為C(B、C不重合).連接CB,CP.
(1)當m=3時,求點A的坐標及BC的長;
(2)當m>1時,連接CA,問m為何值時CA⊥CP?
(3)過點P作PE⊥PC且PE=PC,問是否存在m,使得點E落在坐標軸上?若存在,求出所有滿足要求的m的值,并定出相對應的點E坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車在剎車后行駛的距離s(單位:米)與時間t(單位:秒)之間的關系得部分數據如下表:
時間t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
行駛距離s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
假設這種變化規律一直延續到汽車停止.
(1)根據這些數據在給出的坐標系中畫出相應的點;
(2)選擇適當的函數表示s與t之間的關系,求出相應的函數解析式;
(3)①剎車后汽車行駛了多長距離才停止? ②當t分別為t1 , t2(t1<t2)時,對應s的值分別為s1 , s2 , 請比較 ![]() 與
與 ![]() 的大小,并解釋比較結果的實際意義.
的大小,并解釋比較結果的實際意義.
查看答案和解析>>
科目:初中數學 來源: 題型:
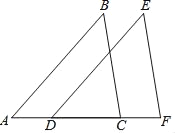
【題目】完成下列證明過程.
如圖,已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求證:△ABC≌△DEF.
證明:∵AB∥DE
∴∠_____=∠_____(_______)
∵AD=CF
∴AD+DC=CF+DC即_____
在△ABC和△DEF中AB=DE_____
∴△ABC≌△DEF_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com