
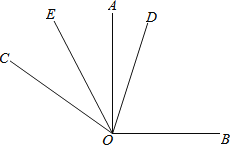
【題目】如圖,已知同一平面內∠AOB=90°,∠AOC=60°.
(1)問題發現:∠BOD的余角是 ,∠BOC的度數是 ;
(2)拓展探究:若OD平分∠BOC,OE平分∠AOC,則∠DOE的度數是 ;
(3)類比延伸:在(2)條件下,如果將題目中的∠AOB=90°改為∠AOB=2∠β;∠AOC=60°改為∠AOC=2α(α<45°),其他條件不變,你能求出∠DOE嗎?若能,請你寫出求解過程:若不能,請說明理由.
【答案】(1)∠AOD,150°;(2)45°;(3)∠DOE=β,理由詳見解析.
【解析】
(1)直接根據余角的定義得到∠BOD的余角,利用∠BOC=∠AOB+∠AOC求出即可;
(2)利用角平分線的性質和(1)中所求得出答案即可;
(3)根據角平分線的性質求出即可.
(1)∵∠AOB=90°,
∴∠AOD+∠BOD=90°,
∴∠BOD的余角是∠AOD,
∵∠AOC=60°,
∴∠BOC=∠AOB+∠AOC=90°+60°=150°,
故答案為:∠AOD,150°;
(2)∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=![]() ∠BOC=75°,∠COE=
∠BOC=75°,∠COE=![]() ∠AOC=30°,
∠AOC=30°,
∴∠DOE的度數為:∠COD﹣∠COE=45°;
故答案為:45°;
(3)∵∠AOB=2β°,∠AOC=2α,
∴∠BOC=2β+2α,
∵OD、OE平分∠BOC,∠AOC,
∴∠DOC=![]() ∠BOC=β+α,∠COE=
∠BOC=β+α,∠COE=![]() ∠AOC=α,
∠AOC=α,
∴∠DOE=∠COD﹣∠COE=β+α﹣α=β.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】下面兩個多位數1248624…… ,6248624…… ,都是按照如下方法得到的:將第一位數字乘以2,若積為一位數,將其寫在第2位上,若積為兩位數,則將其個位數字寫在第2位.對第2位數字再進行如上操作得到第3位數字……,后面的每一位數字都是由前一位數字進行如上操作得到的.當第1位數字是3時,仍按如上操作得到一個多位數,則這個多位數前100位的所有數字之和是( )
A. 495 B. 497 C. 501 D. 503
查看答案和解析>>
科目:初中數學 來源: 題型:
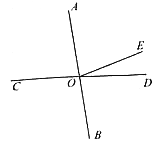
【題目】如圖,AB、CD交于點O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(題中所說的角均是小于平角的角).
(1)求∠AOE的度數;
(2)請寫出∠AOC在圖中的所有補角;
(3)從點O向直線AB的右側引出一條射線OP,當∠COP=∠AOE+∠DOP時,求∠BOP的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
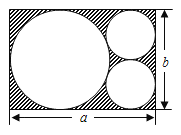
【題目】如圖,在一張長為a、寬為b的長方形紙片上,剪掉一個大圓和兩個半徑相等的小圓.
(1)列出剩余紙片(圖中陰影部分)面積的代數式;(結果要求化簡)
(2)當a=6cm,b=4cm時,求陰影部分的面積,(π取3.14)
查看答案和解析>>
科目:初中數學 來源: 題型:
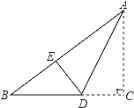
【題目】如圖,一張紙片的形狀為直角三角形,其中∠C=90°,AC=12cm,BC=16cm,沿直線AD折疊該紙片,使直角邊AC與斜邊上的AE重合,則CD的長為______cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形ABCD,過D作BD的垂線,與BC延長線交于E點,F為BE的中點,連接DF,已知DF=4,設AB=x,AD=y,求代數式x2+(y﹣4)2的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
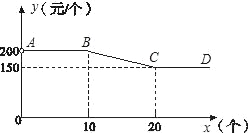
【題目】永定土樓是世界文化遺產“福建土樓”的組成部分,是閩西的旅游勝地.“永定土樓”模型深受游客喜愛.圖中折線(AB∥CD∥x軸)反映了某種規格土樓模型的單價y(元)與購買數量x(個)之間的函數關系.
(1)求當10≤x≤20時,y與x的函數關系式;
(2)已知某旅游團購買該種規格的土樓模型總金額為2625元,問該旅游團共購買這種土樓模型多少個?(總金額=數量×單價)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:n=p×q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解,并規定:F(n)=![]() ,例如12可以分解成1×12,2×6或3×4,因為12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因為12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=![]() .
.
(1)如果一個正整數a是另外一個正整數b的平方,我們稱正整數a是完全平方數,求證:對任意一個完全平方數m,總有F(m)=1.
(2)如果一個兩位正整數t,t=10x+y(1≤x≤y≤9,x,y為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為18,那么我們稱這個數t為“吉祥數”,求所有“吉祥數”中F(t)的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店銷售A型和B型兩種型號的電腦,銷售一臺A型電腦可獲利120元,銷售一臺B型電腦可獲利140元.該商店計劃一次購進兩種型號的電腦共100臺,其中B型電腦的進貨量不超過A型電腦的3倍.設購進A型電腦x臺,這100臺電腦的銷售總利潤為y元.
(1)求y與x的關系式;
(2)該商店購進A型、B型電腦各多少臺,才能使銷售利潤最大?
(3)若限定商店最多購進A型電腦60臺,則這100臺電腦的銷售總利潤能否為13600元?若能,請求出此時該商店購進A型電腦的臺數;若不能,請求出這100臺電腦銷售總利潤的范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com