已知關于x的一元二次方程x2+2(k-1)x+k2-1=0有兩個不相等的實數根x1,x2.
(1)求實數k的取值范圍;
(2)若3(x1+x2)=x1x2,求k的值.
【答案】
分析:(1)根據一元二次方程有兩個不相等的實數根,得出△=b
2-4ac的值大于0,建立關于k的不等式,解不等式即可求出k的取值范圍;
(2)根據一元二次方程的根與系數的關系可以得到x
1+x
2=-2(k-1),x
1x
2=k
2-1,再將它們代入3(x
1+x
2)=x
1x
2,即可求出k的值.
解答:解:(1)△=[2(k-1)]
2-4(k
2-1)
=4k
2-8k+4-4k
2+4
=-8k+8.
∵原方程有兩個不相等的實數根,
∴-8k+8>0,
解得 k<1,
即實數k的取值范圍是 k<1;
(2)由根與系數的關系,x
1+x
2=-2(k-1),x
1x
2=k
2-1,
∵3(x
1+x
2)=x
1x
2,
∴-6(k-1)=k
2-1,
化簡得k
2+6k-7=0,
(k-1)(k+7)=0
∴k=1或k=-7,
又∵k<1,
∴k=-7.
點評:本題考查了一元二次方程ax
2+bx+c=0根的判別式和根與系數的關系的應用,用到的知識點:
(1)△>0?方程有兩個不相等的實數根;
(2)△=0?方程有兩個相等的實數根;
(3)△<0?方程沒有實數根;
(4)x
1+x
2=-
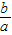
;
(5)x
1•x
2=
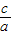
.

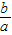 ;
;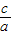 .
. 

 閱讀快車系列答案
閱讀快車系列答案 .
. .
.