【題目】已知，
是一元二次方程
的兩個實數根，且
，拋物線
的圖象經過點
，
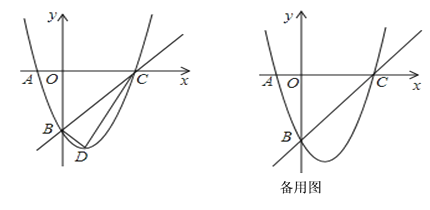
，如圖所示．
（1）求這個拋物線的解析式；
（2）設（1）中的拋物線與
軸的另一個交點為
，拋物線的頂點為
，試求出點，的坐標，并判斷
的形狀；
（3）點
是直線
上的一個動點（點不與點
和點重合），過點作軸的垂線，交拋物線于點
，點
在直線上，距離點為
個單位長度，設點的橫坐標為
，
的面積為
，求出與之間的函數關系式．
【答案】（1）
；（2）
，
，
是直角三角形；（3）當
時，
，當
或
時，
．
【解析】
（1）先解一元二次方程，然后用待定系數法求出拋物線解析式；
（2）先解方程求出拋物線與
軸的交點，再判斷出
和
都是等腰直角三角形，從而得到結論；
（3）先求出
，再分兩種情況，當點
在點
上方和下方，分別計算即可．
解（1）
，
，
，
，
是一元二次方程
的兩個實數根，且
，
，
，
拋物線
的圖象經過點
，
，
，
，
拋物線解析式為，
（2）令
，則
，
，
，
，
，
頂點坐標，
過點
作
軸，
，
，
和都是等腰直角三角形，
，
，
是直角三角形；
（3）如圖，
，，
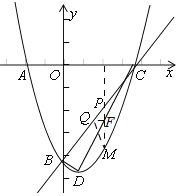
直線
解析式為
，
點的橫坐標為
，
軸，
點的橫坐標為，
點在直線上，點在拋物線上，
，
，
過點
作
，
是等腰直角三角形，
，
，
當點在點上方時，即時，
，
，
如圖3，當點在點下方時，即或時，
，
．
綜上所述：當點在點上方時，即時，，當點在點下方時，即或時，．
閱讀快車系列答案科目：初中數學 來源： 題型：
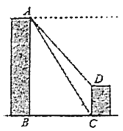
【題目】如圖，甲、乙兩座建筑物的水平距離
為
，從甲的頂部
處測得乙的頂部
處的俯角為48°，測得底部
處的俯角為58°，求乙建筑物
的高度.（參考數據：
，
，
，
.結果取整數）
查看答案和解析>>
科目：初中數學 來源： 題型：
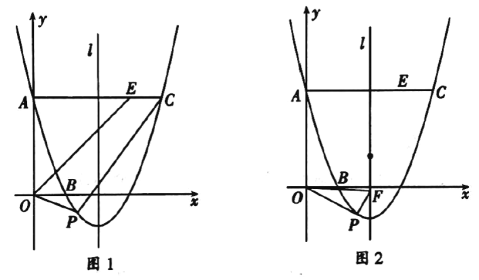
【題目】如圖，已知拋物線
的圖像經過點
，
，其對稱軸為直線
：
，過點
作
軸交拋物線于點
，
的平分線交線段
于點
，點
是拋物線上的一個動點，設其橫坐標為
．
(1)求拋物線的解析式;
(2)如圖1，動點在直線
下方的拋物線上，連結
，當為何值時，四邊形
面積最大，并求出其最大值，
(3)如圖②，
是拋物線的對稱軸上的一點，連接
，在拋物線
軸下方的圖像上是否存在點使
滿足:①
；②
？若存在，求點的坐標，若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
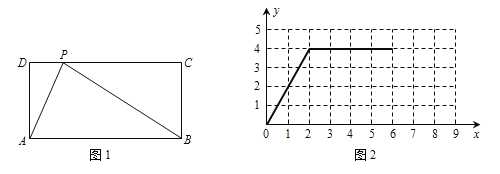
【題目】如圖1，在矩形ABCD中，動點P從點A出發，沿A→D→C→B的路徑運動．設點P運動的路程為x，△PAB的面積為y．圖2反映的是點P在A→D→C運動過程中，y與x的函數關系．請根據圖象回答以下問題：
（1）矩形ABCD的邊AD=________，AB=________；
（2）寫出點P在C→B運動過程中y與x的函數關系式，并在圖2中補全函數圖象．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB為⊙O的直徑，弦CD⊥AB，垂足為點P，直線BF與AD延長線交于點F，且∠AFB＝∠ABC．
（1）求證：直線BF是⊙O的切線；
（2）若CD＝2
，BP＝1，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
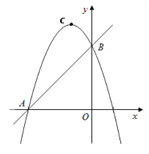
【題目】如圖，拋物線
過點
， 
． 
為線段OA上一個動點（點M與點A不重合），過點M作垂直于x軸的直線與直線AB和拋物線分別交于點P、N．
（1）求直線AB的解析式和拋物線的解析式；
（2）如果點P是MN的中點，那么求此時點N的坐標；
（3）如果以B，P，N為頂點的三角形與
相似，求點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝AC，以AB為直徑的⊙O分別交AC，BC于點D，E，點F在AC的延長線上，且∠BAC＝2∠CBF．
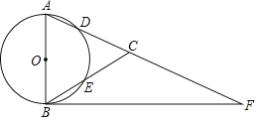
（1）求證：BF是⊙O的切線；
（2）若⊙O的直徑為3，sin∠CBF＝
，求BC長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
與
軸交于點
，與
軸交于點
（點
與點
不重合），拋物線
經過點
，拋物線的頂點為
．
（1）
°；
（2）求
的值；
（3）在拋物線上是否存在點
，能夠使
？如果存在，請求出點
的坐標；如果不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
