
【題目】如圖,已知菱形ABCD的邊長為2,∠B=60°,點P、Q分別是邊BC、CD上的動點(不與端點重合),且BP=CQ.

(1)圖中除了△ABC與△ADC外,還有哪些三角形全等,請寫出來;
(2)點P、Q在運動過程中,四邊形APCQ的面積是否變化,如果變化,請說明理由;如果不變,請求出面積;
(3)當點P在什么位置時,△PCQ的面積最大,并請說明理由.
【答案】(1)△ABP≌△ACQ,△APC≌△AQD;(2)不變,![]() ;(3)點P是BC的中點時.
;(3)點P是BC的中點時.
【解析】
試題(2)根據三角形全等的條件進行判定;
(2)因為△ABP≌△ACQ,所以四邊形APCQ的面積與△ABC的面積相等,沒有發生變化;
(3)當點P是BC的中點時,△PCQ的面積最大.
(1)△ABP≌△ACQ,△APC≌△AQD.
(2)面積不變(1分).因為△ABP≌△ACQ,所以四邊形APCQ的面積與△ABC的面積相等,即四邊形APCQ的面積為![]() .
.
(3)當點P是BC的中點時,△PCQ的面積最大.先說明△APQ是等邊三角形,當點P是BC的中點時,AP垂直于BC,AP最小,此時△APQ的面積也就最小.故在四邊形APCQ的面積一定,△APQ面積最小時,△PCQ的面積最大.


科目:初中數學 來源: 題型:
【題目】“國際無煙日”來臨之際,小敏同學就一批公眾對在餐廳吸煙所持的三種態度(徹底禁煙、建立吸煙室、其他)進行了調查,并把調查結果繪制成如圖所示統計圖,請根據圖中的信息回答下列問題:

(1)被調查者中,不吸煙者中贊成“徹底禁煙”的人數有______人;
(2)本次抽樣調查的樣本容量為_______;
(3)被調查中,希望建立吸煙室的人數有______;
(4)某市現有人口約30萬人,根據圖中的信息估計贊成在餐廳徹底禁煙的人數約有______萬人。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】O為直線AB上的一點,OC⊥OD,射線OE平分∠AOD.

(1)如圖①,判斷∠COE和∠BOD之間的數量關系,并說明理由;
(2)若將∠COD繞點O旋轉至圖②的位置,試問(1)中∠COE和∠BOD之間的數量關系是否發生變化?并說明理由;
(3)若將∠COD繞點O旋轉至圖③的位置,探究∠COE和∠BOD之間的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一數值轉換器,原理如圖所示,若開始輸入x的值是7,可發現第1次輸出的結果是12,第2次輸出的結果是6,第3次輸出的結果是 ,依次繼續下去…,第2013次輸出的結果是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某沿海城市A接到臺風警報,在該城市正南方向260 km的B處有一臺風中心,沿BC方向以15 km/h的速度向C移動,已知城市A到BC的距離AD=100 km,那么臺風中心經過多長時間從B點移動到D點?如果在距臺風中心30 km的圓形區域內都將受到臺風的影響,正在D點休息的游人在接到臺風警報后的幾小時內撤離才可以免受臺風的影響?
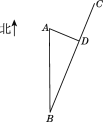
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△AOB繞著一點旋轉到△A′OB′的位置,可以看到點A旋轉到點A′,OA旋轉到OA′,∠AOB旋轉到∠A′OB′,這些都是互相對應的點、線段和角.已知∠AOB=30°,∠AOB′=10°,那么點B的對應點是點______;線段OB的對應線段是線段_____;∠A的對應角是______;旋轉中心是點_______;旋轉的角度是______度.
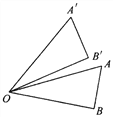
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的二次函數y=x2-(2m-1)x+m2+3m+4.
(1)探究m取不同值時,二次函數y的圖象與x軸的交點的個數情況;
(2)設二次函數的圖象與x軸的交點為A(x1,0),B(x2,0),且x12+x22=5,與y軸的交點為C,它的頂點為M,求直線CM的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD是BC邊上的高,AE、BF分別是∠BAC、∠ABC的平分線,∠BAC=50°,∠ABC=60°,則∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,
中,![]() ,
,![]() 分別在
分別在![]() 軸正半軸和
軸正半軸和![]() 軸負半軸上,
軸負半軸上,![]() 在第二象限,滿足:
在第二象限,滿足:![]() ,
,![]() .已知
.已知![]() .
.
(1)求![]() ,
,![]() 的坐標;
的坐標;
(2)求點![]() 的坐標及
的坐標及![]() 的面積;
的面積;
(3)已知![]() 是
是![]() 軸的正半軸上一點,
軸的正半軸上一點,![]() ,
,![]() 在第一象限,
在第一象限,![]() ,
,![]() ,連接
,連接![]() 交
交![]() 軸于點
軸于點![]() .
.
①求證:![]() .
.
②在點![]() 的移動過程中,給出以下兩個結論:(i)
的移動過程中,給出以下兩個結論:(i)![]() 的值不變;(ii)
的值不變;(ii)![]() 的值不變,其中有且只有一個是正確的,請你找出這個結論并求其值.
的值不變,其中有且只有一個是正確的,請你找出這個結論并求其值.
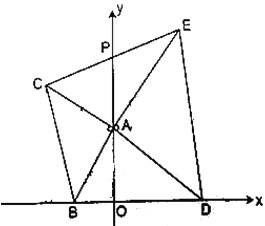
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com