
【題目】如圖,正方形ABCD的邊AB在數軸上,數軸上點A表示的數為﹣1,正方形ABCD的面積為16.

(1)數軸上點B表示的數為 ;
(2)將正方形ABCD沿數軸水平移動,移動后的正方形記為A′B′C′D′,移動后的正方形A′B′C′D′與原正方形ABCD重疊部分的面積為S.
①當S=4時,畫出圖形,并求出數軸上點A′表示的數;
②設正方形ABCD的移動速度為每秒2個單位長度,點E為線段AA′的中點,點F在線段BB′上,且BF=![]() BB′.經過t秒后,點E,F所表示的數互為相反數,直接寫出t的值.
BB′.經過t秒后,點E,F所表示的數互為相反數,直接寫出t的值.
【答案】(1)-5;(2)①點A'表示的數為﹣4或2;②t=4
【解析】試題分析:(1)利用正方形ABCD的面積為16,可得AB長,再根據AO=1,進而可得點B表示的數;
(2)①先根據正方形的面積為16可得邊長為4,當S=4時,分兩種情況:正方形ABCD向左平移,正方形ABCD向右平移,分別求出數軸上點A′表示的數;
②當正方形ABCD延數軸負方向運動時,點E、F表示的數均為負數,不可能互為相反數,不符合題意;當點E、F所表示的數互為相反數時,正方形ABCD延數軸正方向運動,再根據點E、F所表示的數互為相反數,列出方程即可求出t的值.
試題解析:(1)∵正方形ABCD的面積為16,
∴AB=4,
∵點A表示的數為﹣1,
∴AO=1,
∴BO=5,
∴數軸上點B表示的數為﹣5,
故答案為:﹣5.
(2)①∵正方形的面積為16,
∴邊長為4,
當S=4時,分兩種情況:
若正方形ABCD向左平移,如圖1,
A'B=4÷4=1,
∴AA'=4﹣1=3,
∴點A'表示的數為﹣1﹣3=﹣4;
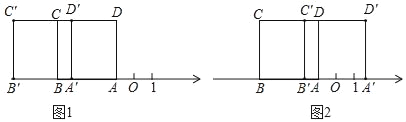
若正方形ABCD向右平移,如圖2,
AB'=4÷4=1,
∴AA'=4﹣1=3,
∴點A'表示的數為﹣1+3=2;
綜上所述,點A'表示的數為﹣4或2;
②t的值為4.
理由如下:
當正方形ABCD沿數軸負方向運動時,點E,F表示的數均為負數,不可能互為相反數,不符合題意;
當點E,F所表示的數互為相反數時,正方形ABCD沿數軸正方向運動,如圖3,
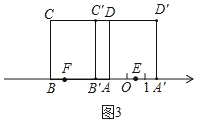
∵AE=![]() AA'=
AA'=![]() ×2t=t,點A表示﹣1,
×2t=t,點A表示﹣1,
∴點E表示的數為﹣1+t,
∵BF=![]() BB′=
BB′=![]() ×2t=
×2t=![]() t,點B表示﹣5,
t,點B表示﹣5,
∴點F表示的數為﹣5+![]() t,
t,
∵點E,F所表示的數互為相反數,
∴﹣1+t+(﹣5+![]() t)=0,
t)=0,
解得t=4.


科目:初中數學 來源: 題型:
【題目】在一次“尋寶”游戲中,已知尋寶圖上兩標志點A和點B的坐標分別為(-3,0),(5,0),“寶藏”分別埋在C(3,4)和D(-2,3)兩點.
(1)請建立平面直角坐標系,并確定“寶藏”的位置;
(2)計算四邊形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】人們在長期的數學實踐中總結了許多解決數學問題的方法,形成了許多光輝的數學想法,其中轉化思想是中學教學中最活躍,最實用,也是最重要的數學思想,例如將不規則圖形轉化為規則圖形就是研究圖形問題比較常用的一種方法。
問題提出:求邊長分別為![]() 的三角形面積。
的三角形面積。
問題解決:在解答這個問題時,先建立一個正方形網格(每個小正方形的邊長為1),再在網格中畫出邊長分別為![]() 的格點三角形△ABC(如圖①),AB=
的格點三角形△ABC(如圖①),AB=![]() 是直角邊為1和2的直角三角形斜邊,BC=
是直角邊為1和2的直角三角形斜邊,BC=![]() 是直角邊分別為1和3的直角三角形的斜邊,AC=
是直角邊分別為1和3的直角三角形的斜邊,AC=![]() 是直角邊分別為2和3 的直角三角形斜邊,用一個大長方形的面積減去三個直角三角形的面積,這樣不需求△ABC的高,而借用網格就能計算出它的面積。
是直角邊分別為2和3 的直角三角形斜邊,用一個大長方形的面積減去三個直角三角形的面積,這樣不需求△ABC的高,而借用網格就能計算出它的面積。
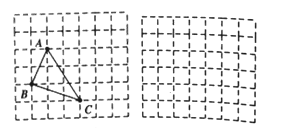
(1)請直接寫出圖①中△ABC的面積為_______________ 。
(2)類比遷移:求邊長分別為![]() 的三角形面積(請利用圖②的正方形網格畫出相應的△ABC,并求出它的面積)。
的三角形面積(請利用圖②的正方形網格畫出相應的△ABC,并求出它的面積)。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,對于任意兩點A(x1,y1)B (x2,y2),規定運算:
(1)A⊕B=(x1+x2,y1+y2);
(2)A⊙B=x1x2+y1y2;
(3)當x1=x2且y1=y2時,A=B.
有下列四個命題:
①若有A(1,2),B(2,﹣1),則A⊕B=(3,1),A⊙B=0;
②若有A⊕B=B⊕C,則A=C;
③若有A⊙B=B⊙C,則A=C;
④(A⊕B)⊕C=A⊕(B⊕C)對任意點A、B、C均成立.
其中正確的命題為______(只填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利用我們學過的知識,可以導出下面這個形式優美的等式:
a2+b2+c2-ab-bc-ac=![]() [(a-b)2+(b-c)2+(c-a)2],
[(a-b)2+(b-c)2+(c-a)2],
該等式從左到右的變形,不僅保持了結構的對稱性,還體現了數學的和諧、簡潔美.
(1)請你檢驗這個等式的正確性;
(2)若a=2 016,b=2 017,c=2 018,你能很快求出a2+b2+c2-ab-bc-ac的值嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列7個事件中:(1)擲一枚硬幣,正面朝上.(2)從一副沒有大小王的撲克牌中抽出一張恰為黑桃.(3)隨意翻開一本有400頁的書,正好翻到第100頁.(4)天上下雨,馬路潮濕.(5)你能長到身高4米.(6)買獎券中特等大獎.(7)擲一枚正方體骰子,得到的點數<7.其中(將序號填入題中的橫線上即可)確定事件為________;不確定事件為________;不可能事件為________;必然事件為________;不確定事件中,發生可能性最大的是________,發生可能性最小的是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),∠AOB=45°,點P、Q分別是邊OA,OB上的兩點,且OP=2cm.將∠O沿PQ折疊,點O落在平面內點C處.
(1)①當PC∥QB時,OQ= ;
②當PC⊥QB時,求OQ的長.
(2)當折疊后重疊部分為等腰三角形時,求OQ的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的對角線相交于點O,∠CAB的平分線分別交BD、BC于E、F,作BH⊥AF于點H,分別交AC、CD于點G、P,連結GE、GF.
(1)求證:△OAE≌△OBG.
(2)試問:四邊形BFGE是否為菱形?若是,請證明;若不是,請說明理由.
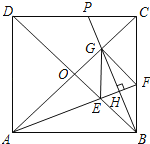
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com