
【題目】利用我們學過的知識,可以導出下面這個形式優美的等式:
a2+b2+c2-ab-bc-ac=![]() [(a-b)2+(b-c)2+(c-a)2],
[(a-b)2+(b-c)2+(c-a)2],
該等式從左到右的變形,不僅保持了結構的對稱性,還體現了數學的和諧、簡潔美.
(1)請你檢驗這個等式的正確性;
(2)若a=2 016,b=2 017,c=2 018,你能很快求出a2+b2+c2-ab-bc-ac的值嗎?
科目:初中數學 來源: 題型:
【題目】如圖,已知∠BAC=40°,把△ABC繞著點A順時針旋轉,使得點B與CA的延長線上的點D重合,連接CE.
(1)△ABC旋轉了多少度?
(2)連接CE,試判斷△AEC的形狀.
(3)若∠ACE=20°,求∠AEC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)-23+![]() (2018+3)0-
(2018+3)0-![]() ; (2)992-69×71;
; (2)992-69×71;
(3) ![]() ÷(-3xy); (4)(-2+x)(-2-x);
÷(-3xy); (4)(-2+x)(-2-x);
(5)(a+b-c)(a-b+c); (6)(3x-2y+1)2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,點![]() 是線段
是線段![]() 所在平面內任意一點,分別以
所在平面內任意一點,分別以![]() 、
、![]() 為邊,在
為邊,在![]() 同側作等邊
同側作等邊![]() 和等邊
和等邊![]() ,聯結
,聯結![]() 、
、![]() 交于點
交于點![]() .
.
(1)如圖1,當點![]() 在線段
在線段![]() 上移動時,線段
上移動時,線段![]() 與
與![]() 的數量關系是:________;
的數量關系是:________;
(2)如圖2,當點![]() 在直線
在直線![]() 外,且
外,且![]() ,仍分別以
,仍分別以![]() 、
、![]() 為邊,在
為邊,在![]() 同側作等邊
同側作等邊![]() 和等邊
和等邊![]() ,聯結
,聯結![]() 、
、![]() 交于點
交于點![]() .(1)的結論是否還存在?若成立,請證明;若不成立,請說明理由.此時
.(1)的結論是否還存在?若成立,請證明;若不成立,請說明理由.此時![]() 是否隨
是否隨![]() 的大小發生變化?若變化,寫出變化規律,若不變,請求出
的大小發生變化?若變化,寫出變化規律,若不變,請求出![]() 的度數;
的度數;
(3)如圖3,在(2)的條件下,聯結![]() ,求證:
,求證: ![]() 平分
平分![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點D、F、E、G都在△ABC的邊上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度數.(請在下面的空格處填寫理由或數學式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(兩直線平行,同旁內角互補)
∵ ,(已知)
∴∠AGD= (等式性質)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊AB在數軸上,數軸上點A表示的數為﹣1,正方形ABCD的面積為16.

(1)數軸上點B表示的數為 ;
(2)將正方形ABCD沿數軸水平移動,移動后的正方形記為A′B′C′D′,移動后的正方形A′B′C′D′與原正方形ABCD重疊部分的面積為S.
①當S=4時,畫出圖形,并求出數軸上點A′表示的數;
②設正方形ABCD的移動速度為每秒2個單位長度,點E為線段AA′的中點,點F在線段BB′上,且BF=![]() BB′.經過t秒后,點E,F所表示的數互為相反數,直接寫出t的值.
BB′.經過t秒后,點E,F所表示的數互為相反數,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的直角坐標系中,解答下列問題:
(1)分別寫出A、B兩點的坐標;
(2)將△ABC向左平移3個單位長度,再向上平移5個單位長度,畫出平移后的△A1B1C1;
(3)求 △A1B1C1的面積。
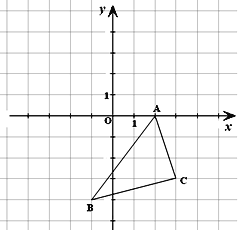
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用直尺和圓規作一個角等于已知角的示意圖如下,則要說明∠D′O′C′=∠DOC,需要證明△D′O′C′≌△DOC,則這兩個三角形全等的依據是__(寫出全等的簡寫).
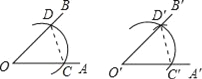
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應國家節能減排的號召,鼓勵居民節約用電,各省先后出臺了居民用電“階梯價格”制度,如下表是某省的電價標準(每月).例如:方女士家5月份用電500度,電費=180×0.6+220×二檔電價+100×三檔電價=352元;李先生家5月份用電460度,交費316元.請問表中二檔電價、三檔電價各是多少?
階梯 | 電量 | 電價 |
一檔 | 0~180度 | 0.6元/度 |
二檔 | 181~400度 | 二檔電價 |
三檔 | 401度及以上 | 三檔電價 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com