Question

12．如圖，在四邊形ABCD中，AC=BD=6，E、F、G、H分別是AB、BC、CD、DA的中點，則EG²+FH²的值為（　　）

• A． 9
• B． 18
• C． 36
• D． 48

Answer 1

分析 作輔助線，構建四邊形EFGH，證明它是菱形，利用對角線互相垂直和勾股定理列等式，再利用中位線性質等量代換可得結論．

解答 解：連接EF、FG、GH、EH，
∵E、F、G、H分別是AB、BC、CD、DA的中點，
∴EF∥AC，HG∥AC，EF=$\frac{1}{2}$AC，FG=$\frac{1}{2}$BD，
∴EF∥HG，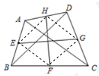
同理EH∥FG，
∴四邊形EFGH為平行四邊形，
∵AC=BD，
∴EF=FG，
∴平行四邊形EFGH為菱形，
∴EG⊥FH，EG=2OG，FH=2OH，
∴EG²+FH²=（2OE）²+（2OH）²=4（OE²+OH²）=4EH²=4×（$\frac{1}{2}$BD）²=6²=36；
故選C．

點評 本題考查了中點四邊形，運用了三角形中位線的性質，將三角形和四邊形有機結合，把邊的關系由三角形轉化為四邊形中，可以證明四邊形為特殊的四邊形；對于線段的平方和可以利用勾股定理來證明．