(1)證明:∵△=a
2-4(a-2)=a
2-4a+8=(a-2)
2+4>0,
∴不論a為何實數,此方程總有兩個不相等的實數根.
(2)解:設x
1、x
2是y=x
2+ax+a-2=0的兩個根,則x
1+x
2=-a,x
1•x
2=a-2,
∵兩交點的距離是

,
∴|x
1-x
2|=
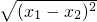
=

.
即:(x
1-x
2)
2=13,
變形為:(x
1+x
2)
2-4x
1•x
2=13,
∴(-a)
2-4(a-2)=13,
整理得:(a-5)(a+1)=0,
解方程得:a=5或-1,
又∵a<0,
∴a=-1,
∴此二次函數的解析式為y=x
2-x-3.
(3)解:設點P的坐標為(x
0,y
0),
∵函數圖象與x軸的兩個交點間的距離等于

,
∴AB=

,
∴S
△PAB=

AB•|y
0|=

,
∴
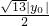
=

即:|y
0|=3,
解得:y
0=±3,
當y
0=3時,x
02-x
0-3=3,即(x
0-3)(x
0+2)=0,
解此方程得:x
0=-2或3,
當y
0=-3時,x
02-x
0-3=-3,即x
0(x
0-1)=0,
解此方程得:x
0=0或1,
綜上所述,所以存在這樣的P點,P點坐標是(-2,3)或(3,3)或(0,-3)或(1,-3).
分析:(1)由△=a
2-4(a-2)=a
2-4a+8=(a-2)
2+4>0,即可判定不論a為何實數,此方程總有兩個不相等的實數根;
(2)首先設x
1、x
2是y=x
2+ax+a-2=0的兩個根,則x
1+x
2=-a,x
1•x
2=a-2,由兩交點的距離是

,可得:(x
1-x
2)
2=13,即可得(x
1+x
2)
2-4x
1•x
2=13,繼而求得a的值;
(3)首先設點P的坐標為(x
0,y
0),由AB=

,△PAB的面積為
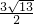
,即可求得y
0的值,繼而求得P點坐標.
點評:此題屬于二次函數的綜合題,考查了根的判別式、根與系數的關系、兩點間的距離公式以及點與二次函數的關系.此題難度較大,注意掌握方程思想的應用.

 時,求出此二次函數的解析式;
時,求出此二次函數的解析式;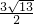 ?若存在求出P點坐標,若不存在請說明理由.
?若存在求出P點坐標,若不存在請說明理由. ,
,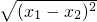 =
= .
. ,
, ,
, AB•|y0|=
AB•|y0|= ,
,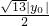 =
=
 ,可得:(x1-x2)2=13,即可得(x1+x2)2-4x1•x2=13,繼而求得a的值;
,可得:(x1-x2)2=13,即可得(x1+x2)2-4x1•x2=13,繼而求得a的值; ,△PAB的面積為
,△PAB的面積為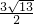 ,即可求得y0的值,繼而求得P點坐標.
,即可求得y0的值,繼而求得P點坐標.

 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案